THE P(R) DISTRIBUTION

タンパク質またはRNAのような希釈された非相互作用粒子に関するSAXSは、2点間距離分布関数 P（r） 関数を測定する。 P（r） 関数は、散乱体内の2点間のすべての距離のヒストグラムを表す。 SAXS測定は分解能が限定されており、この限定された分解能のこの分布関数のサンプリングと考えることができる。分布関数は実空間で測定されるため、x軸はオングストローム単位である。分布関数は滑らかで非負であり、粒子の最大寸法でゼロに近づくと考えられる。 SAXSでは、 P（r） 関数は、高分子構造内のすべての電子間の距離対を記述するために使用され、巨大分子内の構造変化を視覚的に検出するための有用なツールである。この関数は、ある構造内のすべての2点間距離を記述しているため、少数の残基の相対位置の小さな変化は、 P（r） 関数の検出可能な変化をもたらし得る。

次の図に示すように、T7 RNAポリメラーゼは、転写開始に備えて酵素がドメイン再配列を起こす。物体の散乱質量は変化しないが、領域の相対位置の変化は、 P（r） 関数（シアンからオレンジ）の変化と同様にそれぞれの散乱プロファイルの変化を生じる。

図

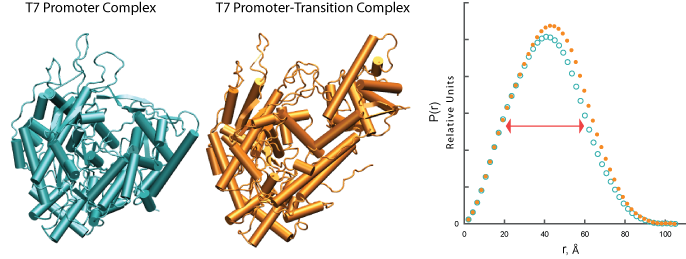
したがって、ドメインの相対位置の変化は、その重心の周りのタンパク質の質量分布とその回転半径 Rg を変化させる。 Rg は、 r のすべての値にわたって関数を r ² と積分することによって P（r） 関数から得ることができる。したがって、2つの異なる条件からの高分子の Rg の比較は、条件の違いによる立体配座変化を明らかにすることができる。あるいは、 Rg は、典型的なSAXS実験からのデータの小さなサブセットを利用するGuinier近似によって得ることができる。前者の方法とは異なり、 P（r） 関数から計算された Rg はすべての実験データを使用し、実空間で決定される（ P（r） 関数の横座標の単位に注意）。 P（r） に基づく回転半径は一般に「実空間」 Rg と呼ばれる。

BACKGROUND

Peter Debyeは最初に、ルーサイトのような固体内の誘電体の不均一性の観点から可視光散乱を記述した。彼の定式化は、距離ベクトル ｒ を変化させて決められる「相関関数」を利用した。その関数は入射角に比例するある距離の不均一性に関係している。もし、入射散乱波長がX線である場合、相関関数と P（r） 関数には直接的な関係がある。

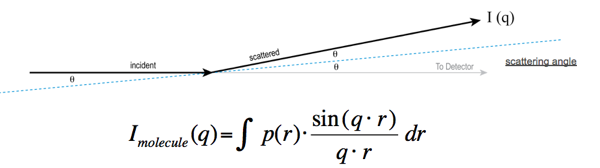
上記の式は、単一の高分子の P（r） 関数を散乱角 q の関数としての散乱強度と関連付ける。従って、ある散乱角 q における観測された散乱強度は、物体内距離 r の全値にわたる sinc 関数 \(（\sin qr）/ qr\) と P（r） 関数との積の積分である。

さらに、高分子サンプルの挙動を理解するのに役立つ P（r） 関数内にいくつかの定性的特徴が存在する。詳細については、Putnam、C.D.、et al。によるレビュー参照。

Pr_review Putnam、C.D.、Hammel、M.、Hura、G.L.、and Tainer、J.A。 Q Rev Biophys。 2007 40（3）：191-285注：

T7プロモーター複合体（ 1cez.pdb ）およびT7プロモーター - 転移複合体（ 1msw.pdb ）の P（r） 関数関数を、Crysol および Gnom を用いてシミュレートした。 SAXSの計算に先立って、非タンパク質成分はそれぞれのpdbファイルから削除された。