P（R）-DISTRIBUTION

SCÅTTER は、データを実空間に変換するために修正Moore関数 1 を使用する。 ノイズを軽減するために、P（r） 関数の二次導関数にL1-ノルム規格化拘束を課する。 滑らかさの拘束は最終的にMoore係数に課される。 さらに、SAXSデータにMoore関数をフィットさせるために、残差の中央値を最小化するShannon限定サンプリング法を提供している。 サンプリング法のパラメータは、 “Setting” タブ（図1）にある。 正則化の強さはλ（デフォルト0.01）によって制御される。 ノイズの多いデータセットは、 C を大きくすることによって変換できる。 C （デフォルト2）は、滑らかさを評価するために使用されるポイントの数を効果的に増やす。 比較のために、GNOMは〜101の等間隔データポイントを使用して滑らかさを評価する。

図1

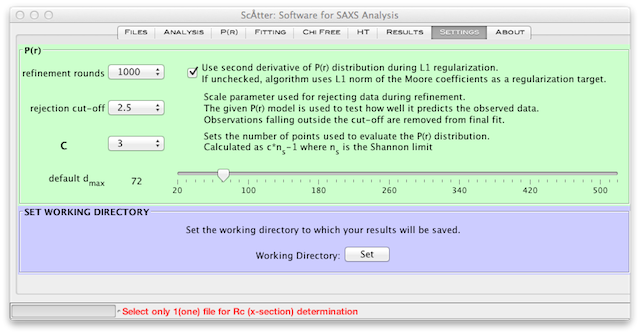
../_images/4.1pr_figure_1-852829a8007faca0e369fdc973c0d8c1.png

ほとんどのデータセットでは約2000回の “Pr_refinement rounds”　が必要である（図1）。 “Pr_refinement rounds”　は、P（r） 決定中に使用されるフィットおよびサブサンプリングの数を表す。ノイズの多いデータセットには3,000〜4,000回のラウンドが必要である。サブサンプリングの間、このソフトは効果的にパラメータ空間を探索し、この検索結果を使用してでのデータのサブセットがデータセット全体を最もよく説明するかどうかを判断することができる。これは、SAXSデータセットが高度にオーバーサンプリングされているため可能である（Rambo and Tainer Nature 496、477-481 (2013)を参照）。選択のカットオフは “REjection cut-off” によって設定され、本質的に標準偏差カットオフとして機能し、標準化された残基がカットオフの外側データポイントが最終フィットから除外されることを意味する。

デフォルトのパラメータを使用して、データセットをロードし、“Analysis” タブに切り替える。ここでは、 SRNA_2.dat という名前のデータセットを使用（図2）。 SRNA_2.dat は特に困難なデータセットで、リフォールディングステップで生成されたミスフォールドRNAを含むRNA種の混合物である。 “Guinier Rg” または “Auto Rg” ボタンを使用してGuinierのパラメータが決定されていることを確認する。左下の青い “REAL SPACE” ラベルの下にある “P(r)” ボタンをクリックする。また、 P（r） 決定の際、データを q と q * I（q） としてプロットすることを勧める。このSAXSデータの表現は、フーリエ空間で使用されるデータの形式を示す（ “SVD Reduce” ボタンのすぐ隣）。

図2

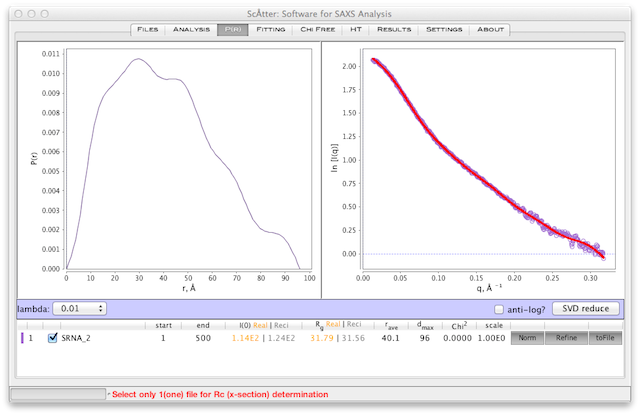
../_images/pr_figure_2.png

“P(r)” ボタンは “P(r)” タブに切り替わり、 “Setting” タブ（図1）で指定した dmax （デフォルト：96）を使用して予備適合を実行する。私たちは滑らかな（あまり多くの塊ではない） P（r） 分布を求める。ここには、多くのこぶがあり、終点は不連続である。 dmax が小さすぎるように見える。

P（r） - 関数は、間接フーリエ変換（IFT）法を用いて決定される。 IFTは、P（r） - 関数を実空間のSAXSデータをモデル化するための代表的な関数（正弦関数またはZernike系列または他の基底関数など）で近似する。代表関数のパラメータは、最小自乗法などのフィッティングルーチンによって決定される。 Scatterは、解を安定化するために、L1ノルムの規格化項で解を安定化するconvex最適化法（内点）を使用する。規格化には2つの方法がある：1）Moore係数の絶対和を最小にすることと、2） P（r） 分布の平滑さを最大にすること。規格化の選択は、 “Setting” タブ（図3、オレンジ色の矢印）で行うことができる。方法1は、最小バイアスと見なせる。

図3

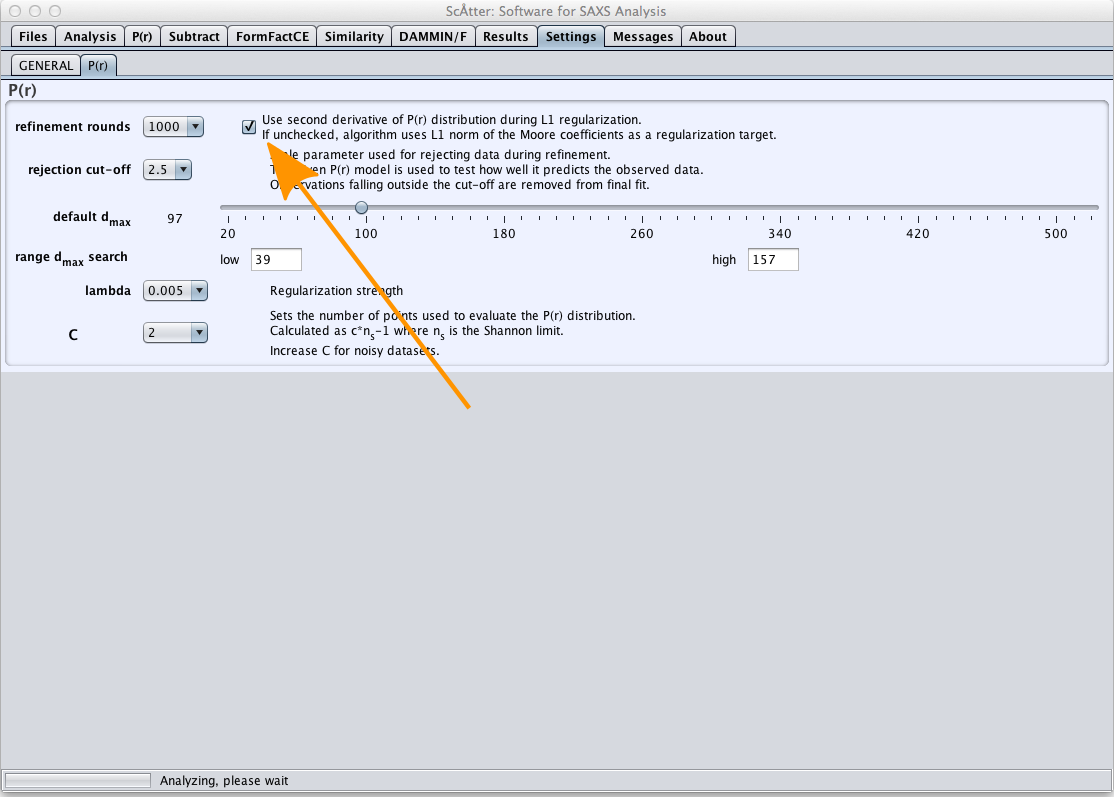
../_images/4.3pr_figure_1a.png

まず、 “Start” ボックス（図4）を使用して最初の10〜20ポイントをトリミングすることを勧める。通常、SAXSデータセットのGuinier領域全体が削除される。これは、ギニア領域が疑わしいサンプルでは重要であり、サンプル中の凝集の影響を弱めるために使用される。 Guinier領域はIFTにとって不可欠ではなく、IFT法は欠落した情報を補間する。よく振る舞うサンプルとデータセットは、Guinier領域の有無にかかわらず決定された P（r） 関数間に大きな違いを示すべきでない。

図4

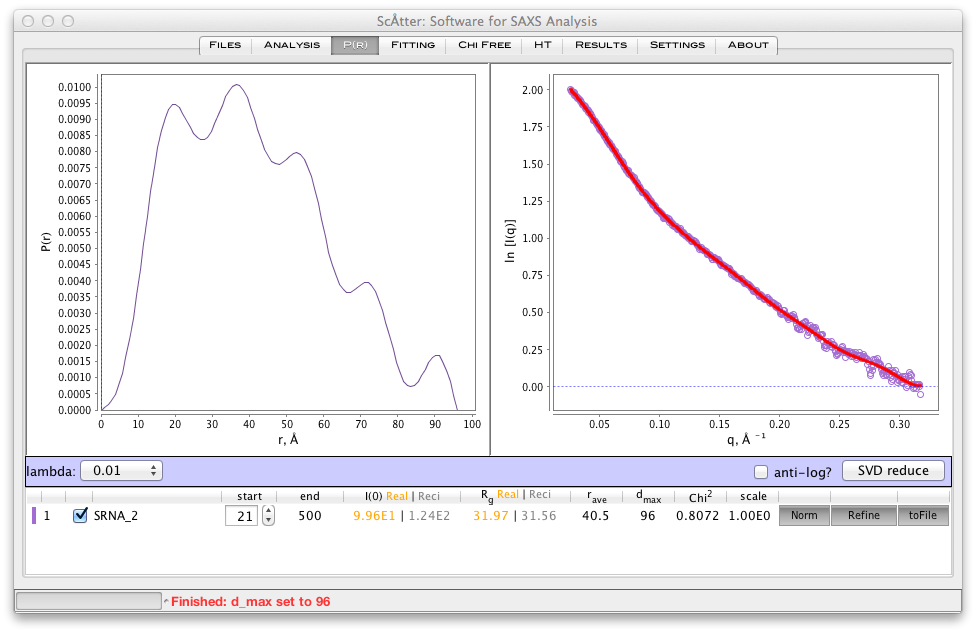
../_images/4.4pr_figure_3-afeba09c9e336daa98fe20ceeb988c96.png

最初の〜10点を除去した後、うねりははるかに深刻である（図4）。ここでは、dmax ボックスの上向き矢印をクリックして dmax を増やす。

図5

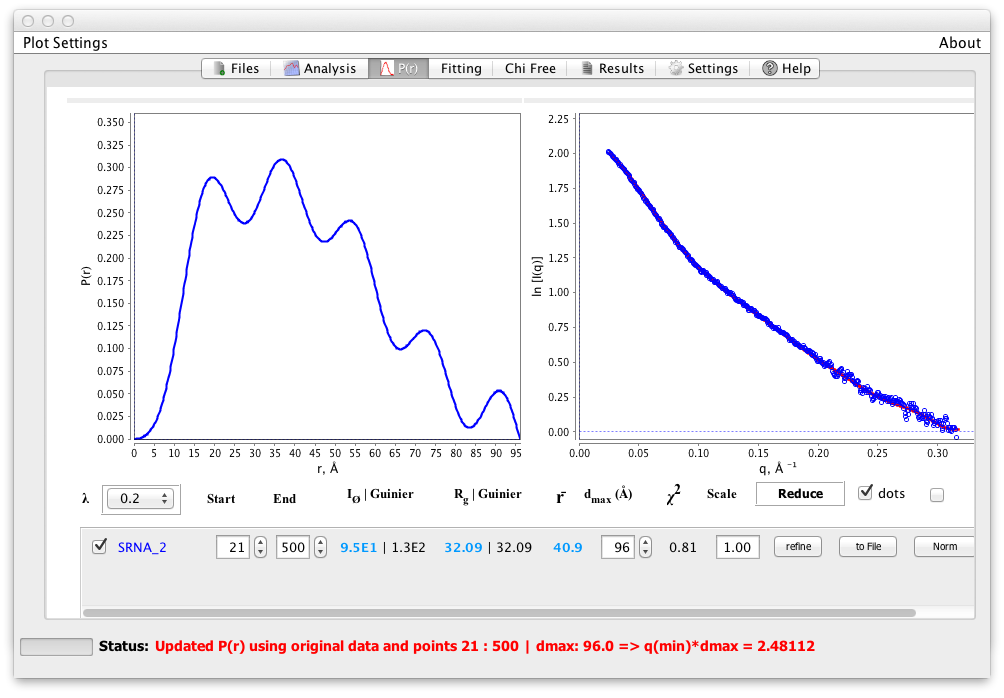
../_images/4.5pr_figure_4-0f15d9e9b3336bff0be67d4648a4e486.png

大部分の起伏が滑らかになるまで dmax を増加させる。我々は、滑らかで正の関数をもたらす最大の dmax を選択する傾向がある。いかなる負の値も避ける。ここでは、113の dmax を確定した（図5）。 Chi-squaredは1に近く、S k2 はできるだけ小さくする必要がある。これらの値はよく見えるため, “refine” ボタンを使用して解をテストできる。

図5

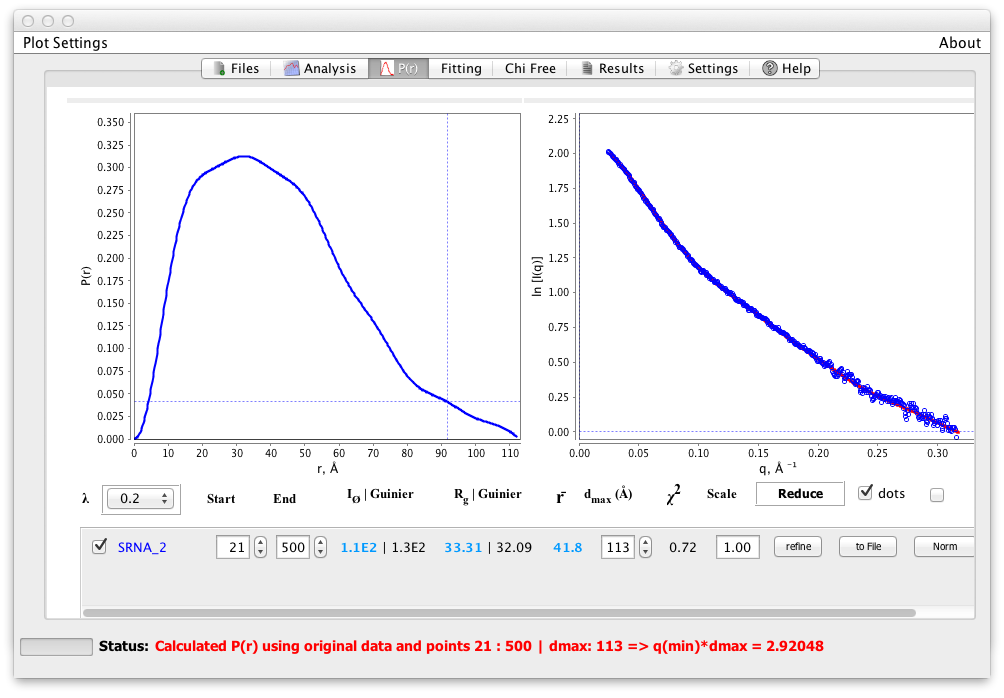
../_images/4.6pr_figure_5-380f7a269ffa9483236c78fcebaa0859.png

dmax で設定した後、 “refine” ボタンを押す。これは、データが dmax によって定義された基礎となる P（r） 関数とどのくらい一貫しているかを決定。前に述べたように、ここでは “pr_refinement rounds” と “rejection cut-off” が最適化で使用されている。

図5a：

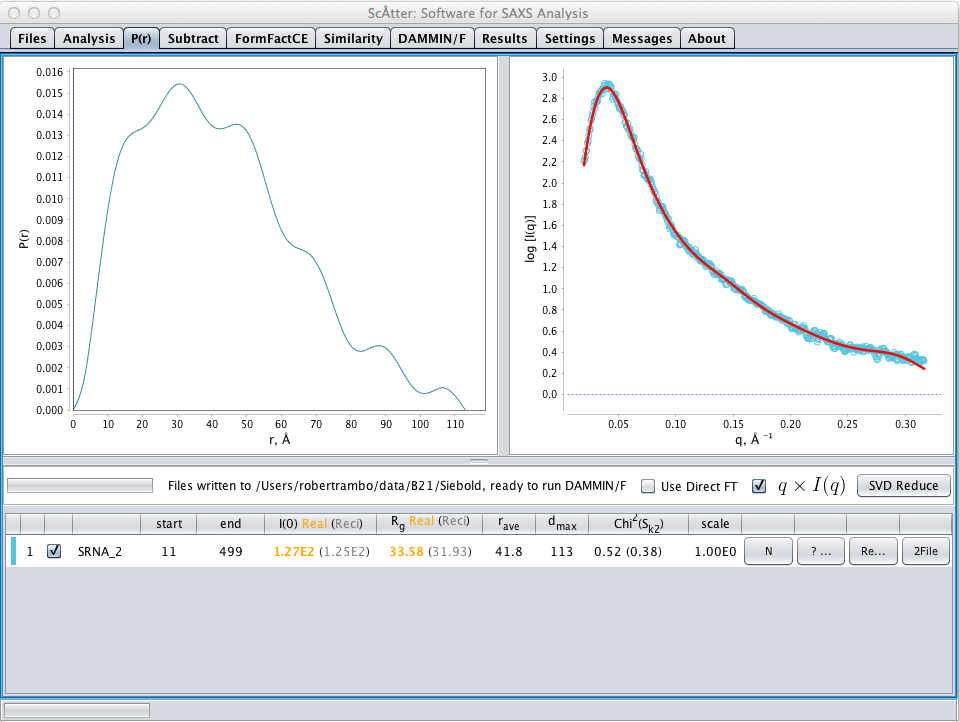
../_images/4.7pr_figure_5a.png

ここでは、 P（r） 関数が悪化していることが分かる。この関数はこの dmax によって完全には定義されておらず、ｘ 2 乗は小さすぎる（<1）。 “Use second derivative”　（図2を参照）をチェックし、異なる dmax を113回Å近傍でテストすることによって、分布に平滑化拘束を課すことができる。

図6：

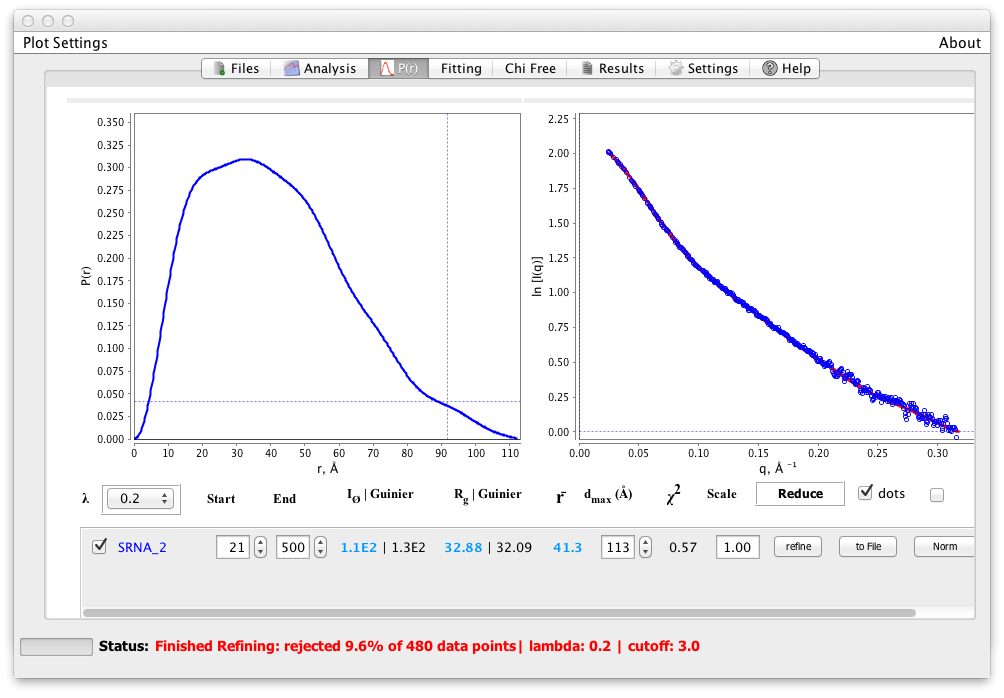
../_images/4.8pr_figure_6-73458e64c4468a2405d169415e63158d.png

dmax を118に設定し、ポイントの約10％が削除して最適化を実行するとポイントの約10％が削除され（図6）、スムーズではあるが正の P（r） 関数になった。 Chi 2 はわずかに高いが、これは1に近いカイ二乗と0に近いS k2 で滑らかさを最大にする解を見つけることとの間に良い妥協である。洗練されたデータセットは自動的にGNOMで使用するためにファイルに書き込まれ、次に DAMMIN / F または GASBOR で使用される。

質の悪いバッファー差分は、 P（r） の決定を困難にする。 dmax を決定する際に問題がある場合は、データをより低い分解能で切り捨ててみるとよい。