NORMALIZED KRATKY

無次元(正規化)のKratkyプロットは、溶液中の生体高分子の状態を評価するための半定量的アプローチを提供します。 天然変性タンパク質(IDP)に対する応用性では、Receveur-BrechotとDurandを参照するか、Rambo and Tainer(生体高分子)の一般的な検討事項を参照してください。 このプロットは q ベクトル(X軸)に粒子の Rg を掛け、q2の代わりに \(I(q)\) に \((q\cdot Rg)^2\) を掛けることにより無次元化されます(Durand D,Vives C,et al,2010を参照)。 粒子の質量および濃度を正規化するために、無次元化された \(I(q)\) を実験の \(I(0)\) により除算します。 ギニエの近似に従う粒子については、 \(\sqrt{ 3 }\) の位置で大きさ \(3e^{-1}(1.104)\) のピークが存在します。

ギニエ近似からはじめると：

\[I(q)=I(0) \cdot e^{-\frac{(q \cdot Rg)^2}{3}}\]

\((q \cdot Rg)^2\) を掛け、 \(I(0)\) で割る：

\[(q \cdot Rg)^2 \cdot \frac{I(q)}{I(0)}=(q \cdot Rg)^2 \cdot e^{-\frac{(q \cdot Rg)^2}{3}}\]

\(u=q \cdot Rg\) として変数の変更を行う：

\[f(u)=(u)^2 \cdot \frac{I(q)}{I(0)}=(u)^2 \cdot e^{-\frac{(u)^2}{3}}\]

微分をとって \(f'(u)=0\) を解くことによって、最初の最大値を求める：

\[f'(u)=2u \cdot e^{-\frac{(u)^2}{3}}-u^2 \cdot \frac{2u}{3} \cdot e^{-\frac{(u)^2}{3}}\]
\[2u \cdot e^{-\frac{(u)^2}{3}}= \frac{(2u)^3}{3} \cdot e^{-\frac{(u)^2}{3}}\]

両辺の平方根をとって、 u または \((q \cdot Rg)=\sqrt{ 3 }\) を解く：

\[3=u^2\]

このタイプの無次元Kratkyプロットは、Guinierの近似に従うのなら、ほとんどの球状のコンパクト粒子に対し、粒子の大きさ、組成および濃度に関わらず \(\sqrt{ 3 }\) の位置で最大値をとります。 このことからの偏差は、粒子の柔軟性または非対称性を示唆しています（Receveur-BrechotおよびDurand（2012）またはDurandら（2010）を参照）。

図１

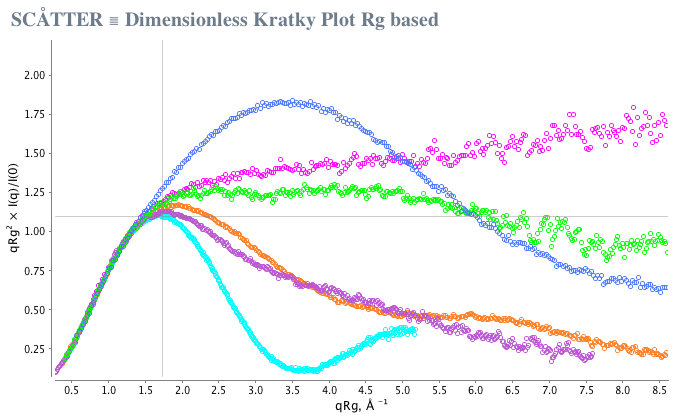
../_images/2.png

図1において、21kDaの球状タンパク質、キシラナーゼ(シアン)は、 \(\sqrt{ 3 }\) の位置でピーク極大を示します。 非対称粒子に関しては、図1：P4-P6 RNAドメイン(オレンジ)およびSAM-1リボスイッチ(紫)を見ると ピークは右にシフトし最大は1.104よりおおきくなります。 天然変性タンパク質(RAD51-AP1)については、古典的な双曲線プラトー(マゼンタ)を得ます。 よく折り畳まれたマルトース結合タンパク質(青色)にRAD51-AP1が結合すると、ピークは右にシフトし \((q \cdot Rg = 3.5)\)、新しい最大値に達します。 Rg ベースの無次元Kratkyプロットは、Guinier解析または実空間変換のいずれかに由来する \(I(0)\) および Rg に基づいています。 実空間パラメータが事前に決定されていれば、SCÅTTERはこれらのプロットを自動的に作成します。 Vcを使用してもう1つの無次元プロットを作成することができます(図2)。 ここでは、プロットを無次元にするために、 \((q \cdot Rg)^2\) の代わりに \(q^2 \cdot Vc\) を使用します。 まだ I(0) に正規化しますが、ピークの高さは \(Vc / Rg^2\) に正比例します。これは粒子の表面積対体積比に反比例する比率です。 一つの球に対する理論上の最大の高さは、0.82になります。

図２

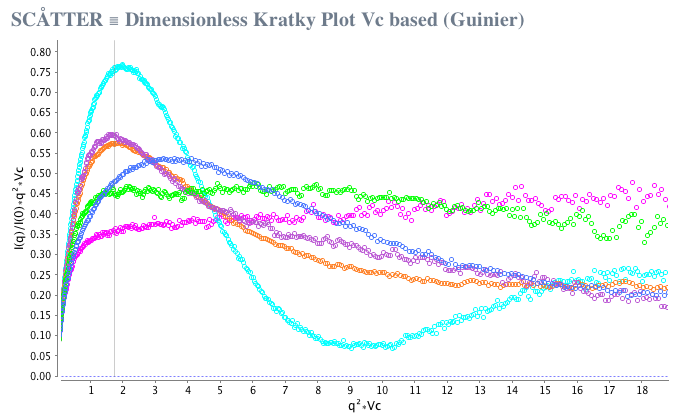
../_images/3.png

この無次元Kratkyプロットの形式は、粒子構造の変化を推測するために、より有益となり得ます。 例えば、SAMリボスイッチを図1および図2の( +、紫)リガンドおよび( - 、緑)リガンドなしと比較してください。 Rgベースのプロットでは、SAM(-)曲線(緑色)がより双曲線であり、柔軟なアンサンブルを示唆するため、立体構造の違いがあることは明らかです。 しかしながら、 Vc ベースのプロット(図2)では、双曲線の特徴はSAM( - )曲線では保たれているが、リガンドの非存在下での粒子の表面積対体積比の増加を示唆する下方にシフトしています。 SCÅTTERは、ボタン “Normal Kratky” （図3、赤い矢印）をクリックするだけで、無次元のKratkyプロットを作成できます。 I(0) と Rg パラメータ、またI I(0) と Vc を使った2つのプロット(実空間と逆数空間)のみを使用して、4つのプロット、2つのプロット(実空間と逆空間)を作成します。

図３

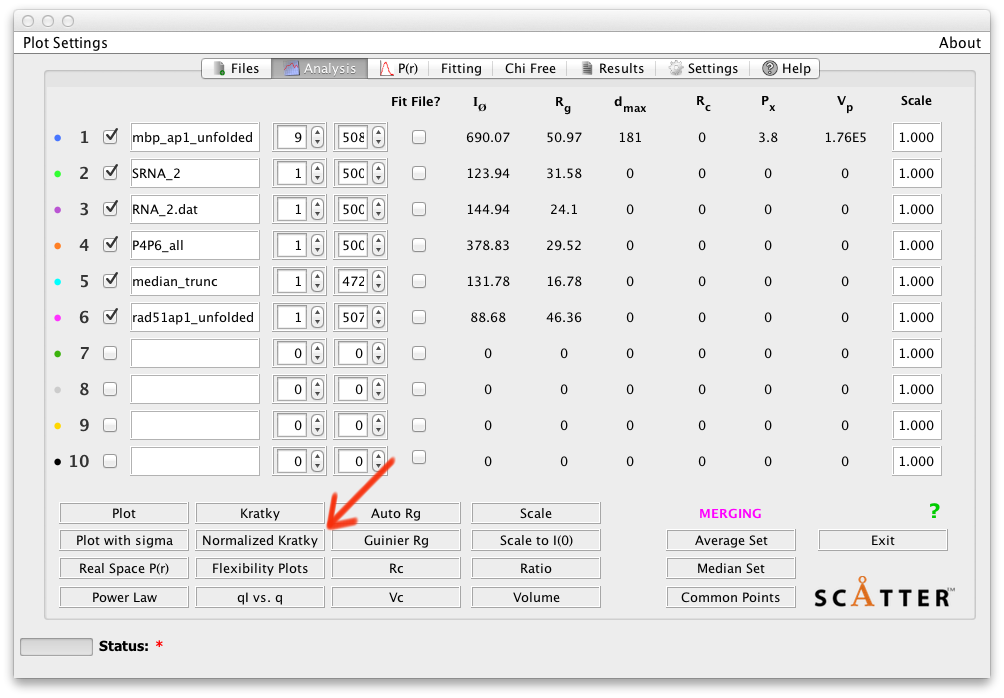
../_images/4.png

注釈

  • これらのプロットは I(0) 、Rg および Vc の決定に敏感である。
  • Guinierプロットを精査する。
  • P(r)関数がギニエ領域に影響されないことを確認する。