プログラミング初歩。
目次
数値処理
目次(ページ内)
プログラミングの初歩
数学
prorama自習用参考情報(更新予定はありません)
プログラミングの初歩
プログラミングの初歩
programaというフリーウェアを書籍では、アルゴリズムの学習用に使用させてもらっています。
SAKURAI's site
N88互換BASIC for Windows95
過去のものとなりつつあるが、それでも、基礎は学ぶには使える。動作がやや遅い。この他にも有料のもので、Basic系のソフトウェアは健在である。
日本語プログラミング環境
■なでしこ(ひまわりの後継言語)
数学
数学
■KIT数学ナビゲーション−金沢工業大学工学基礎教育センター
金沢工業大学での、いわゆるリメディアル教育用の数学基礎教育用のページ
外部にも公開されている。復習に使えるすばらしいサイトです。
■基礎数学ワークブック
高知工科大学の数学教室の井上昌昭教授のすばらしいサイト。
prorama自習用参考情報(更新予定はありません)
問題等の番号が書籍とは多少一致しないことがあります。
1.ラジアンについて未習者・忘失者は、必ず復習してください。
また、問題3と問題5については、演習前までに、以下に記した指定の作業を行っておくこと。
また、自習問題についても計算式の意味を予習しておくこと。
練習問題2(この解説を読めば、習ってない人もわかるはず)
ラジアンは、単位円(半径が1の円)の弧の長さによって角度を表す方法で、度との関係は、1ラジアン=180度/π≒57.3度で、1度=π/180ラジアン≒0.017ラジアンとなる。ラジアンには単位記号がありません。
円周率の定義は、円の直径と円周の長さの比率が一定であることからきており、一定の比率をπ、半径をr、円周をLとすれば、π=L/2r(これが、円周率)。扇形の中心角の大きさと弧の長さは比例するので、半径と同じ長さの弧の長さ持つ扇形の中心角の大きさを1ラジアンと定義します。
すると、半径rのおうぎ形の半円周の長さ(L/2)はπrだから、
πr:r=180(度):1(ラジアン)。式を変形して、1(ラジアン)=180度/π。当然、度を使うかラジアンを使うかで、計算の意味が異なってくることになり、cos60°≠cos60となります。エクセルでも同様ですが、引数(ひきすう)には、ラジアンで入れないと、cos60°は0.5とでてきません。
注意)ただし、私の持っている関数電卓では、cos60°は、そのまま60を入れると、0.5と計算されます。
ケースバイケースの対応が必要です。
問題3
右に入れた計算結果が左に入る。逆はできない。
予め、xとyについて、解いておきましょう。
間違い例)
x+yという変数→計算式を変数にするのは変数自体に指定できません。
x+y=aと2x+4y=bをそのまま書くとなんの計算もされません。
全角の変数も指定できません。また大文字と全角は違う概念です。
半角の大文字もあれば、全角の小文字もあります。
問題5
予め、2点の座標がわかっている場合に、傾きと切片を求める計算式を考えておくこと。
自習問題1と自習問題2
(時間が余れば、演習時間内に行うので、予め計算式を導く背景について学習しておくこと)
この問題は、
1.x=0,y=25の条件と、x=40、y=53の2つの条件をy=b*axに代入する。
2.25=b*a0は、a0が1だから、bは25が得られる。
3.あとはaだけがわからないので、bに25を入れると、53=25a40で、両辺を1/40乗すると、a=(53/25)1/40となる。
4.つまり、これらの値を、y=b*axに代入するとy=25*(53/25)x/40となる。きちんと書くと下のようになる。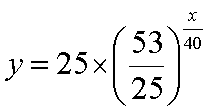
5.しかし、やりたいことは、yが既知の時にxが知りたいので、x=、、、の式に変形する。
両辺にlogを取り、資料にある公式で変形すると、次の式が得られる。
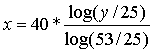
これにyを75(億人)とか100(億人)を入力すると何年後とでるようになる。
2.
プログラムは初めは計算結果がおかしくてもバグや考え違いを少しずつ直していくことで、正解にたどり着きます。多少、計算に変な値がでても、「なぜ」、その変な値がでるのか考えてください(ここが重要)。そこに修正すべきポイントが隠されています。とくに反復を使うようになると、間違った考えが計算結果に顕著に表れます。
Σ(シグマ)記号の数学的意味の未習者・忘失者は、数学的意味を復習してください。
自習問題3の、プロバイダー利用における課金システムを予め、学習しておいてください。
問題8で用いるモンテカルロ法について、予め、学習しておいてください。
練習問題5
式の意味を簡単にプログラミング用に考えおなすところがポイントです。式をそのままプログラミングするのではなく、
どのようなアルゴリズムでプログラミングすると、式を表現できるかを予め、下のヒントを参考に考えておくこと。
1.変数には最初ゼロが格納されているので、nを1から始めるためには、
まずに1を入れる必要がある。 n = 1
2.例えば、nの初期値が1で、Σxという式があるとすると、不定回反復の中に、
x = x + n
n= n + 1
と書いて繰り返せば、1ずつ変数aの値が増加して、Σと同じ役割を果たしています。
指定した反復数だけn=1からの和が求まります
3.Σ(シグマ)の前にある4の値は、Σとは関係ないので、最後に4をかければいいですね。
※テキストにも書いたように、不定回反復の「かつ及びまたは」は、programa自身の中から実行する時(ex.F5を押すなど)は、問題ありません。しかし、Basicのソースファイル出力でうまくいきません。条件の変更は3より大きい値を指定してみると5回ぐらいで計算が止まると思います。3.13ぐらいなら、50回弱です。
自習問題3
MSS社は使用時間にかかわらず、一定の条件で料金計算されるので、利用時間(分)に対して、使用料をかけるだけ。
PDO社は、60分を越えると条件が異なるので、利用時間によって使用料が異なる計算を条件分岐で行う必要がある。
ただし、PDO社はアクセスポイントまでの通信費が常にかかることを忘れずに。
ちなみに、計算すると、30分と90分の時、同額となる。
30分より短いとMSS社が安く、30分を超えて90分に達しない内は、PDO社が安い。
また90分を超えるとMSS社が安くなる。
問題6
練習問題6とほとんど問題として変わらないが、今度は定回反復を使用することだけ
(不定回反復でも反復条件を1000回にすればできますが、、、)。ヒントも重要。
ルートは関数を使用すればよい。
問題8
流れ図にすると、たったこれだけ。下の図を参考にして下さい。
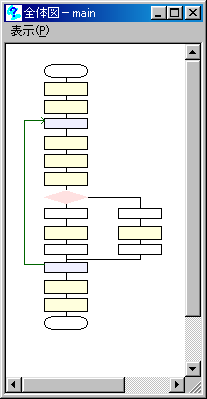
作る順番は、下の番号の2番から1番へと作った方がよいが、考え方は以下のようである。
1.発生させた座標の距離を計算した後に、条件分岐を用いて、
距離が1未満である時にカウントする時は、a = a + 1を行い、距離が1以上である時は、a = aを行うようにすればよい。
そうすると条件によってカウントしたり、カウントしなかったりする部品ができる。
2.上述の処理が繰り返しの中にあるようにする。
この部品で繰り返し数がコントロールできる。
※テキストにも書きましたが、X*X+Y*Yをやらずに、pow関数を使って2乗した人は4がでます。乱数は正しく発生できているのに、rの値が必ずゼロと計算されていますので、pow関数に問題があるかもしれません、、、。完全な原因ははっきりしません(わかりません)。 2回ずつかけることで作成して下さい。
3.カウンタ変数は、普通のプログラミング言語では、カウンタの増加数(刻み)を決めますが、programaでは1ずつとなっています(繰り込み算をすれば、2ずつ増やすこともできます)。
2ずつ増加させたいときは、カウンタ変数が「i」とすると、例えば、「i = i+1」 を繰り返しの中に入れておけば、通常1ずつ増えるので、結果的に2ずつ増えることになります。
これなら、「i」が「0」から始めれば、偶数の配列変数だけを指定できますし、その他、色々応用できます。
Y[i+1] = Y[i] + x のように、
カウンタ変数に四則演算を加えることにできます。逆言うと、しないとできない問題もあるでしょう。
階乗の数学的意味について未習者・忘失者は、予め学習しておいてください。
練習問題8
得点を90で割って、100かけるだけ。
ただし、元の得点が失われては困るので、別の配列変数に値を格納する。
問題10
2回目に作成したプログラムを何回も実行するように改良する。つまり、前回のプログラムをさらに繰り返しの中に入れる必要がある。
1つの得られたπの値を配列変数に格納していく。最終的に、その平均をとればいい。かなり変数を作成しないとダメ。私は10ぐらい使用した。
しかし、流れ図はたったこれだけ
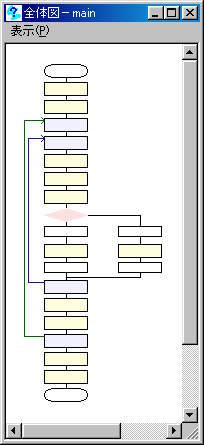
問題11
式2つで、計算が規定されているので、一つの計算式だけではできない。
まず、ゼロの階乗だけを例外(初期値)として作る。
例えば、kaijo[i] = 1(kaijo[0] が1)として、最初にiが0の時の値を格納する。
次に、
n=1の時、n・(n-1)!は、1・0!で、
n=2の時、n・(n-1)!は、2・1!で、
n=3の時、n・(n-1)!は、3・2!で、、、、なので、
kaijo[1](1!)は、1・kaijo[0]で、
kaijo[2](2!)は、2・kaijo[1]で、
kaijo[3](3!)は、3・kaijo[2]で、、、、となっていることになる。だんだん規則性が見えてくる。
これを配列変数で一般式に直す(ここを考えよう)。
考えた式を手計算で、紙の上でプログラムを模擬的に動作させ、そのアルゴリズムがあっているか、
確認する。
あとは、計算と表示で、必要数繰り返すようにすればよい。
最終問題
これはヒントをよく読んで。ヒント以上に解説するのは難しいかも、、、。
ページトップへ戻る