水散乱による絶対強度測定

水散乱による絶対強度測定は、Orthaber et al., J.Appl.Cryst. (2000) 33, 218-225. で記載された方法を用いる。

散乱強度の測定

サンプルを測定する時と同一の条件で以下の測定を行う。

  1. 温度の測定

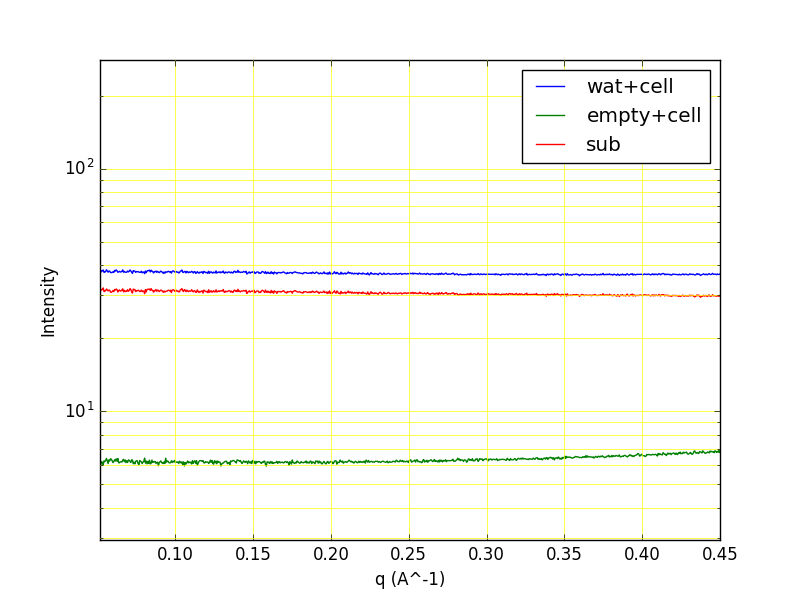
  2. （水＋セル）からの散乱の測定

  3. （空セル）からの散乱の測定

  4. beamstopモニターの値( \(BS\) )と露光時間（ \(Time\) )で補正して（水＋セル）ー（空セル）を行う。

    \[I_{water}(q)_{exp}=\dfrac{I_{water+cell}(q)}{BS\cdot Time}-\dfrac{I_{emptycell}(q)}{BS\cdot Time}\]

  5. \(I_{water}(q)_{exp}\) が比較的一定となる中広角領域の平均強度 \(I_{water}(0)_{exp}\) を求める。

    藤澤研では4.、5.の計算には tk_wat_abs.py を用いる。プログラムにはファイル名だけでなく平均をとるq領域と 測定温度を入力する。

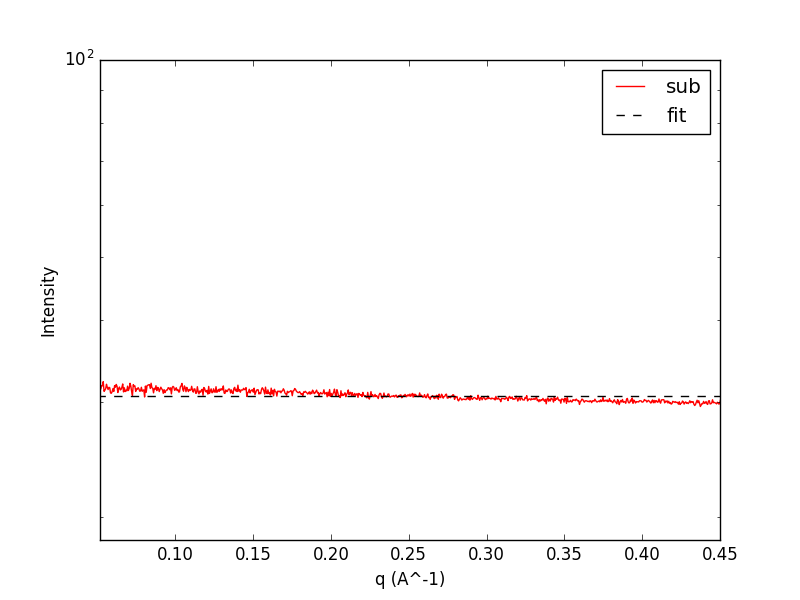
../_images/abs1.png ../_images/abs2.png
（水＋セル）、（空セル）の散乱 \(I_{water}(0)_{exp}\) の近似

  1. 水散乱の標準値を参照 水の広角散乱の値は水の等温圧縮率 \(\chi_T\) と散乱長密度 \(\rho\) の関数で

    \[I_{water}(0)_{theory}=\rho^2kT\chi_T\]

    で与えられる。

    各温度における水の散乱の理論値
    Temperature °C
    \(I(0) \,\,\rm{cm^{-1}}\)
    		 Temperature °C
    \(I(0) \,\,\rm{cm^{-1}}\)
    0 0.01692 20 0.01632
    4 0.0167 25 0.01633
    5 0.01665 30 0.01638
    10 0.01647 35 0.01647
    15 0.01637 40 0.0166

  2. 絶対強度への変換係数 fac の算出

    20℃において、 \(I_{water}(0)_{exp} \,\,\rm{20 C^o}=30.64 \,\,\rm{a.u.}\) だとすると 変換係数 fac は以下の式のようになる。

    \[fac=\dfrac{I_{water}(0)_{standard} \,\,\rm{20 C^o}}{I_{water}(0)_{exp} \,\,\rm{20 C^o}} =\dfrac{0.01632 \,\,\rm{cm^{-1}}}{30.64 \,\,\rm{a.u.}} =5.3264\times 10^{-4} \,\,\rm{cm^{-1}\,a.u.^{-1}}\]

重要

解析ソフトの仕様に注意！

sample散乱からbuffer散乱を差分するソフトの中には、濃度や露光時間で規格化したりしなかったりする。 自作ソフトで *.dat ファイルを作成している人は、強度補正の仕方が異なる場合もあるので注意しよう。

本稿で使用する差分ソフト tk_Pila2dat.py は、 \(Time \times BS\) の積算値で生のデータ値を割り、 体積補正付きで差分したもの重量濃度(mg/ml)で割っている。水の測定の時に、アテニュエーターを外している場合、 \(BS\) の桁数が変わっている場合もあるので留意する。