サンプルの \(I(0)/C\) 決定と MW¶
サンプルの絶対強度測定による分子量の決定は、
対象となる
*.datとがどのように規格化されているか得られた \(I(0)/C\) から以下の式に基づきどのソフトを使って MW を計算するか
\[MW_{sample}=\dfrac{I(0)_{sample}}{c_{sample}} \dfrac{N_A}{(\Delta\rho\nu_{sample})^2}\]ここで、 \(I(0)_{sample}\) 、\(c_{sample}\) はそれぞれ、絶対強度スケールの \(I(0)/C\) 、濃度の単位が \(\rm{g\, cm^{-3}}\) のサンプル濃度を 表す。
によって変わってくる。
ここでは BL45XU-SAXS 標準のソフトにより生成される *.dat と
藤澤研固有の tk_Pila2dat.py により生成される *.dat
の2通りのやり方を紹介する。
サンプルはBSAを例とし、 MULCh から以下のパラメータを得られているとする。
| \(\nu_{sample}\) | \(\rho_{BSA}\) | \(\rho_{buffer}\) | \(\Delta\rho\) | \(I(0)_{sample}/c_{sample}\) |
|---|---|---|---|---|
| \(\rm{cm^3\, g^{-1}}\) | \(\rm{10^{10}\, cm^{-2}}\) | \(\rm{10^{10}\, cm^{-2}}\) | \(\rm{10^{10}\, cm^{-2}}\) | \(\rm{a.u.\, mg^{-1}mL}\) |
| 0.733 | 12.363 | 9.530 | 2.833 | 80.32 |
BL45XU-SAXS 標準のソフトにより生成される *.dat の場合¶
BL45XU-SAXS ではサンプルのデータフォルダの下に analysis
というフォルダが自動的に作成され、その中に subtraction-i2-*.dat という
ファイルが収められる。このファイルは、 BS で生のデータを規格化し、buffer散乱との差分を
行った後、重量濃度 c (mg/ml)で割ったものである。
エクセルで直接計算する場合¶
最初に水で決めた fac を用いて
で \(\rm{mg^{-1}cm^2}\) の単位とし、さらに重量濃度の単位を \(\rm{mg\, cm^{-3}}\) から \(\rm{g\, cm^{-3}}\) に変更する。
エクセルの表で
| \(I(0)_{sample}/c_{sample}\) 相対強度 | \(I(0)_{sample}/c_{sample}\) 絶対強度 | \(I(0)_{sample}/c_{sample}\) 絶対強度 |
|---|---|---|
| \(\rm{a.u. mg^{-1}cm^3}\) | \(\rm{mg^{-1}cm^2}\) | \(\rm{g^{-1}cm^2}\) |
| 80.32 | 0.04278 | 42.78 |
絶対強度の \(I(0)_{sample}/c_{sample}\) が求まれば、
| \(\nu_{sample}\) | \(\Delta\rho\) | \((\Delta\rho\nu_{sample})^2\) |
|---|---|---|
| \(\rm{cm^3g^{-1}}\) | \(\rm{cm^{-2}}\) | \(\rm{g^{-2}cm^2}\) |
| 0.733 | 2.8330E+10 | 4.3122E+20 |
から \((\Delta\rho\nu_{sample})^2\) を求め、上の式に直接代入すれば良い。
RAW を使用する場合¶
RAW では、 fac を設定すると自動的に絶対強度に変換するオプションも存在するが確認していない。 \(I(q)\) は絶対強度に変換して \(I(0)_{sample}/c_{sample}\) の形で 以下のように RAW を使えば良いであろう。
tk_Pila2dat.py により生成される *.dat の場合¶
tk_Pila2dat.py により生成される *_sc.dat は、生のデータを \(BS\times Time\) で割り、差分データは重量濃度 \(c \rm{(mg/ml)}\) で割っている。
すでに絶対スケール \(\rm{(cm^2g^{-1})}\) に変換されている \(I(0)_{sample}/c_{sample}\) である。
エクセルで直接計算する場合¶
上記のように、 \((\Delta\rho\nu_{sample})^2\) を求め計算を行う。単位だけを気をつければよい。
RAW を使用する場合¶
RAW を使えば、ギニエ解析を行って \(I(0)\) 、 Rgを決定すると、絶対強度から 分子量を決定してくれる。また、Porod体積などからの分子量も算出してくれる。 具体的な手順は、
メイン画面からフォルダを選択して、
*.datファイルをloadする。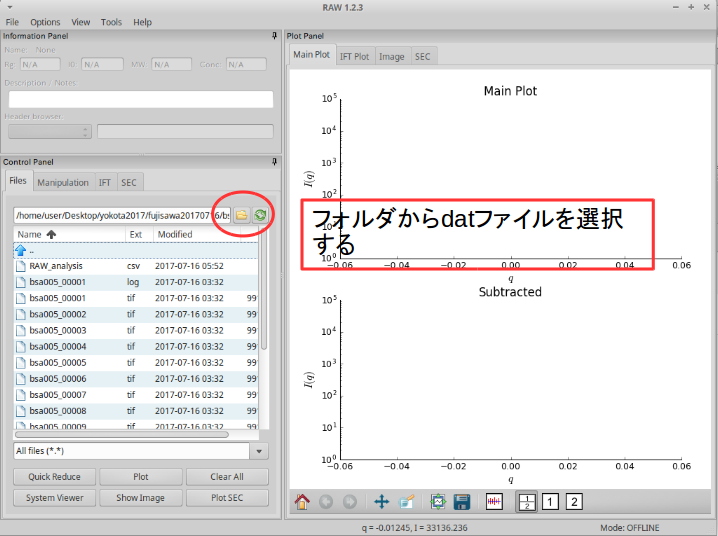
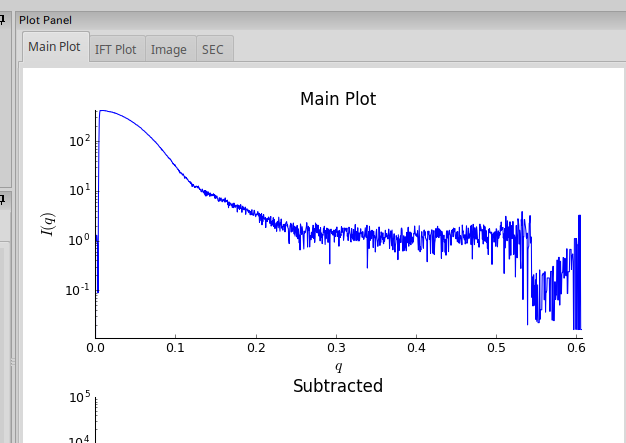
解析するデータ範囲を指定する。
Main Plot画面を右クリックして、Porod plot表示にする。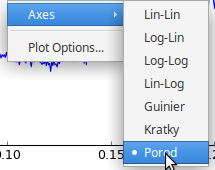
重要なのは広角側をどれだけとるかということであるが、
Porod plotで一定となる領域を指定する。 ついでに小角側の立ち下がりも削除しておく。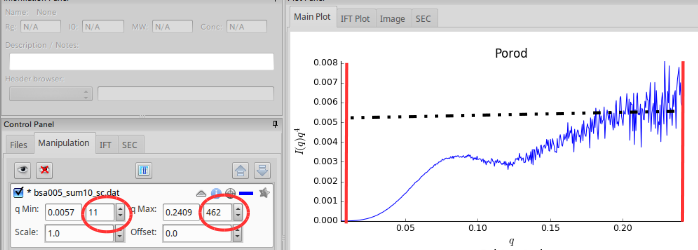
から
loadされたデータを右クリックして ギニエ解析を起動する。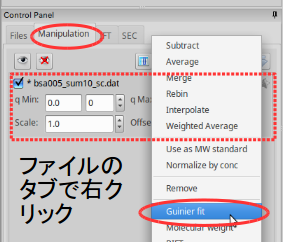
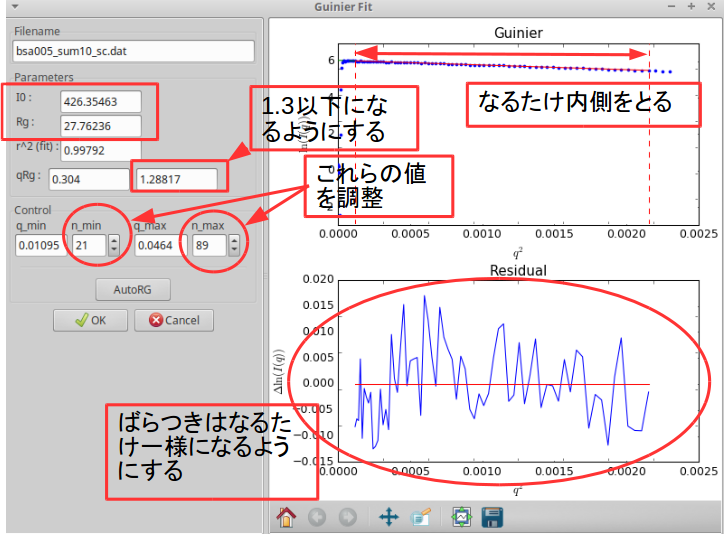
ギニエ領域を指定して、 \(I(0)\) 、 \(Rg\) を得る。
から
loadされたデータを右クリックして GNOM を起動する。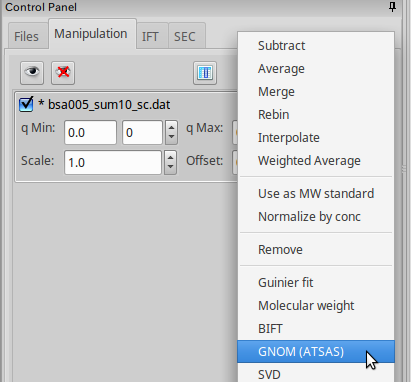
\(P(r)\) 関数の計算領域、
n_min、n_maxを指定して、GNOM saysが 良い応答を示すようDmaxを調整する。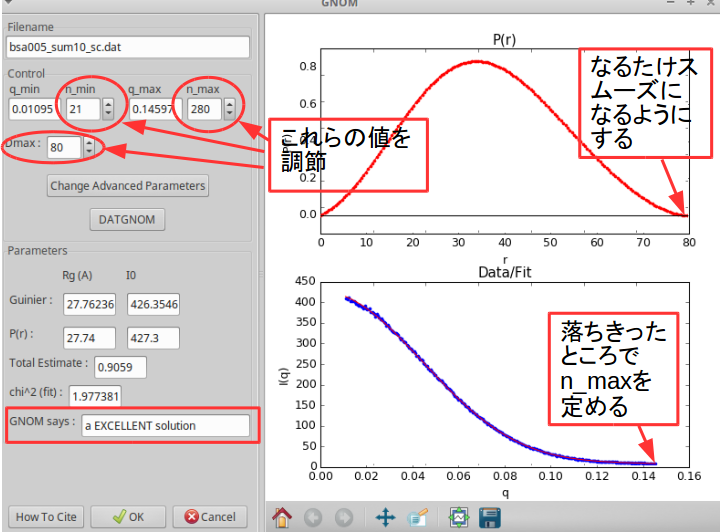
\(I(0)\) 、 \(P(r)\) 関数などを計算した後に、 から
loadされたデータを右クリックして分子量決定タブを起動する。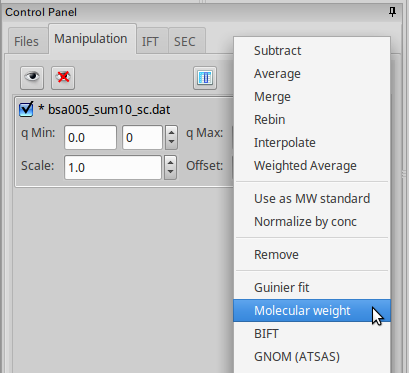
すでに \(I(0)\) 、 \(P(r)\) 関数などを計算しているので、相関体積 \(Vc\) 、Porod体積 \(Vp\) から分子量がそれぞれ
Vc MW、Vp MWとして表示されている。絶対強度による分子量Abs.MWを 表示させるには、 をクリックする。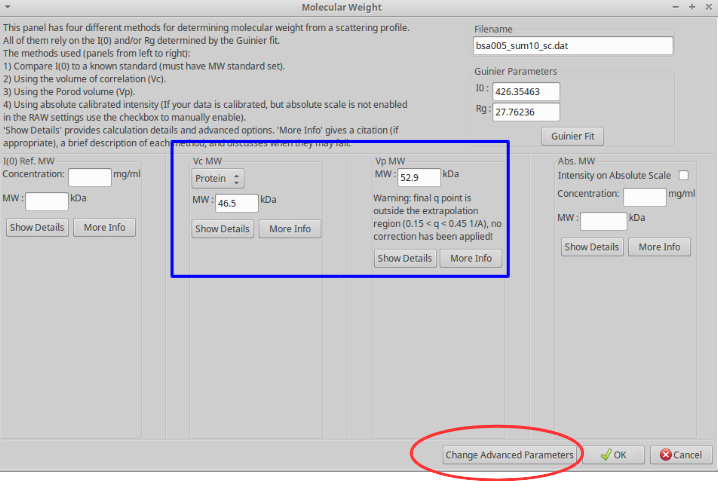
対象となるタンパク質の小角散乱パラメータを設定する。必要な値は以下のとおりである。
Electrons per dry mass of macromolecule\(\rm{(e^{-}g^{-1})}\) :1分子の乾燥重量あたりの電子数これは対象のタンパク質のプロトマーのアミノ酸配列から電子数を計算する。 MULCh は1分子あたりの散乱長 \(\Sigma b_X\) を計算してくれるのでそこから算出する。
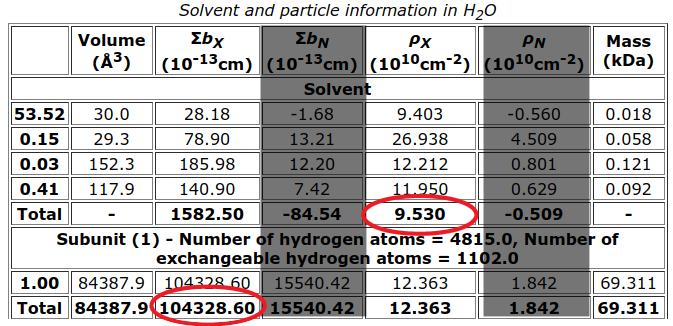
一電子の散乱長は古典電子半径 \(r_0=e^2/m_ec^2=0.28179\times 10^{-12} \rm{cm}\) で与えられるので、 一分子の質量を \(M_1\) とすれば、
\[\Sigma b_x \,\,\rm{(cm)}/r_0 \,\,\rm{(cm)} / M_1 \,\,\rm{(g)}\]Electrons per volume of aqueous solvent\(\rm{(e^{-}cm^{-3})}\) : 溶媒の体積あたりの電子数これは溶媒の散乱長密度 \(\rho_x\) を単位変換すればよい。
\[\rho_x \,\,\rm{(cm^{-2})}/ r_0 \,\,\rm{(cm)}\]PSV of macromolecule\(\rm{(cm^3g^{-1})}\) : タンパク質の偏比容これは、計算値を代入すれば良い
scattering length of an electron\(\rm{(cm/e^{-})}\) : 一電子の散乱長は古典電子半径上に書いたように固定。
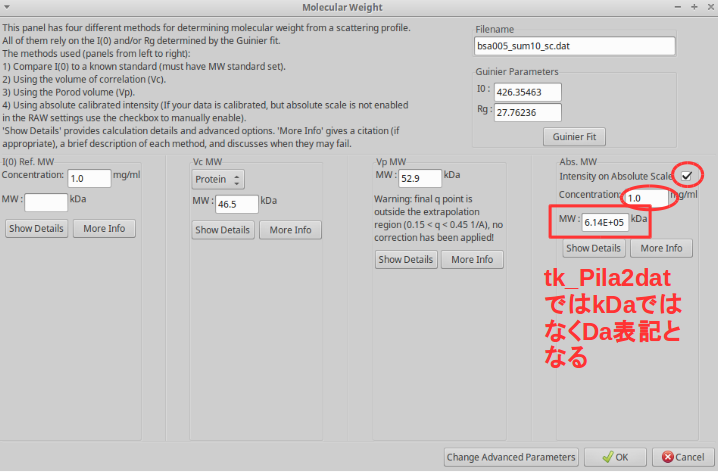
Intensity on the Absolute Scaleをチェックして濃度を入力する。ここでは、1.0を入力する。
重要
tk_Pila2dat.py では、桁落ちを回避するために \(10^3\) かけた変換係数を入力するので
出力される分子量の値は kDa ではなく Da 表記となる。
注釈
RAW でのコントラストは質量あたりの散乱コントラスト \(\Delta\rho_M \,\,\rm{(cm\,g^{-1})}\) である。 いわゆるコントラスト \(\Delta\rho\) とは、 \(\Delta\rho_M=\Delta\rho\nu\) の関係となる。 \(\Delta\rho_M\) は以下の式で求まる。