仮想仕事の原理関係
表面力による仮想仕事
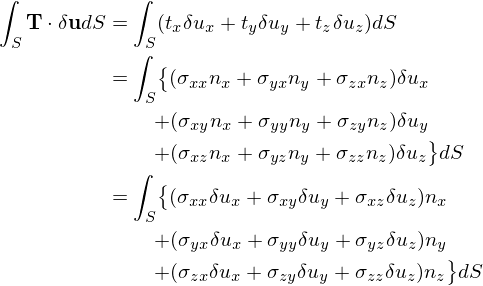
\begin{eqnarray*}
\int_S \mathbf{T}\cdot \delta \mathbf{u}dS&=&\int_S(t_x\delta u_x+t_y\delta u_y +t_z\delta u_z)dS \\
&=&\int _S\bigl\{(\sigma_{xx}n_x+\sigma_{yx}n_y+\sigma_{zx}n_z)\delta u_x \\
&& ~~~~ +(\sigma_{xy}n_x+\sigma_{yy}n_y+\sigma_{zy}n_z)\delta u_y \\
&& ~~~~ +(\sigma_{xz}n_x+\sigma_{yz}n_y+\sigma_{zz}n_z)\delta u_z \bigr\}dS\\
&=&\int _S\bigl\{(\sigma_{xx}\delta u_x +\sigma_{xy}\delta u_y +\sigma_{xz}\delta u_z)n_x\\
&& ~~~~ + (\sigma_{yx}\delta u_x +\sigma_{yy}\delta u_y +\sigma_{yz}\delta u_z)n_y\\
&& ~~~~ + (\sigma_{zx}\delta u_x +\sigma_{zy}\delta u_y +\sigma_{zz}\delta u_z)n_z \bigr\}dS
\end{eqnarray*}
|
コーシーの関係
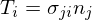
\[
T_i=\sigma_{ji}n_j
\]
|
ガウスの発散定理
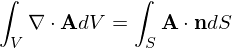
\int _V \nabla \cdot \mathbf{A} dV= \int _S \mathbf{A}\cdot \mathbf {n}dS
|

\[
\int _V
\left(
\frac{\partial f_x}{\partial x}+
\frac{\partial f_y}{\partial y}+
\frac{\partial f_z}{\partial z}
\right)dV=
\int_S(f_xn_x+f_yn_y+f_zn_z)dS
\]
|
表面力による仮想仕事を変形
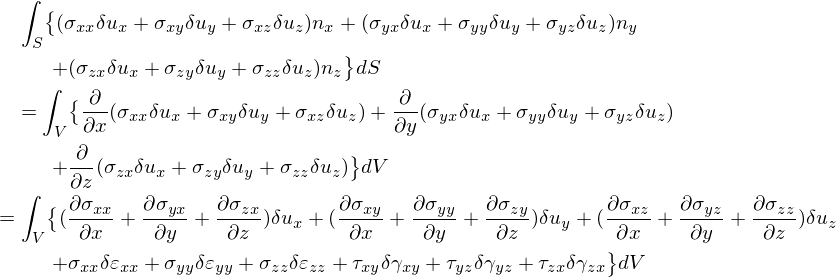
\begin{eqnarray*}
&&\int_S\bigl\{
(\sigma_{xx}\delta u_x+\sigma_{xy}\delta u_y +\sigma_{xz}\delta u_z)n_x +
(\sigma_{yx}\delta u_x+\sigma_{yy}\delta u_y +\sigma_{yz}\delta u_z)n_y \\
&&~~~~~~ +(\sigma_{zx}\delta u_x+\sigma_{zy}\delta u_y +\sigma_{zz}\delta u_z)n_z \bigr\}dS\\
&&=\int_V\bigl\{
\frac{\partial}{\partial x}(\sigma_{xx}\delta u_x+\sigma_{xy}\delta u_y +\sigma_{xz}\delta u_z)+
\frac{\partial}{\partial y}(\sigma_{yx}\delta u_x+\sigma_{yy}\delta u_y +\sigma_{yz}\delta u_z)\\
&&~~~~~~ +\frac{\partial}{\partial z}(\sigma_{zx}\delta u_x+\sigma_{zy}\delta u_y +\sigma_{zz}\delta u_z)\bigr\}dV \\
&=&\int_V \bigl\{
(\frac{\partial\sigma_{xx}}{\partial x}+\frac{\partial\sigma_{yx}}{\partial y}+\frac{\partial\sigma_{zx}}{\partial z})\delta u_x +
(\frac{\partial\sigma_{xy}}{\partial x}+\frac{\partial\sigma_{yy}}{\partial y}+\frac{\partial\sigma_{zy}}{\partial z})\delta u_y +
(\frac{\partial\sigma_{xz}}{\partial x}+\frac{\partial\sigma_{yz}}{\partial y}+\frac{\partial\sigma_{zz}}{\partial z})\delta u_z \\
&&~~~~~~+\sigma_{xx}\delta \varepsilon_{xx}+\sigma_{yy}\delta \varepsilon_{yy} +\sigma_{zz}\delta \varepsilon_{zz}
+\tau_{xy}\delta \gamma_{xy} +\tau_{yz}\delta \gamma_{yz}+ \tau_{zx}\delta \gamma_{zx}\bigr\}dV
\end{eqnarray*}
|
弾性力学
等方線形弾性体のフックの法則
\varepsilon_{ij}=
\frac{1+\nu}{E}
\left(
\sigma_{ij}-\frac{\nu}{1+\nu}\delta_{ij}\sigma_{kk}
\right)
|
FEM
三角形一次要素のBマトリックス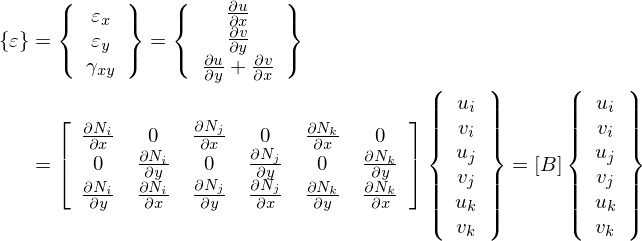
\begin{eqnarray*}
\{\varepsilon\}&=&
\left\{
\begin{array}{c}
\varepsilon_x\\
\varepsilon_y\\
\gamma_{xy}
\end{array}
\right\}=
\left\{
\begin{array}{c}
\frac{\partial u}{\partial x}\\
\frac{\partial v}{\partial y}\\
\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\\
\end{array}
\right\}\\
&=&
\left[
\begin{array}{cccccc}
\frac{\partial N_i}{\partial x} & 0 &
\frac{\partial N_j}{\partial x} & 0 &
\frac{\partial N_k}{\partial x} & 0 \\
0 & \frac{\partial N_i}{\partial y} & 0 &
\frac{\partial N_j}{\partial y} & 0 &
\frac{\partial N_k}{\partial y} \\
\frac{\partial N_i}{\partial y} & \frac{\partial N_i}{\partial x} &
\frac{\partial N_j}{\partial y} & \frac{\partial N_j}{\partial x} &
\frac{\partial N_k}{\partial y} & \frac{\partial N_k}{\partial x} \\
\end{array}
\right]
\left\{
\begin{array}{c}
u_i\\
v_i\\
u_j\\
v_j\\
u_k\\
v_k
\end{array}
\right\}=
[B]\left\{
\begin{array}{c}
u_i\\
v_i\\
u_j\\
v_j\\
u_k\\
v_k
\end{array}
\right\}
\end{eqnarray*}
|
Bマトリックスの成分
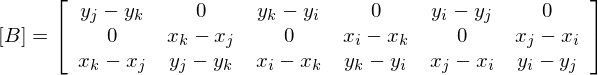
\begin{eqnarray*}
[B]=
\left[
\begin{array}{cccccc}
y_j-y_k & 0 & y_k-y_i & 0 & y_i-y_j & 0 \\
0 & x_k-x_j & 0 & x_i-x_k & 0 & x_j-x_i \\
x_k-x_j & y_j-y_k & x_i-x_k & y_k-y_i & x_j-x_i & y_i-y_j\\
\end{array}
\right]
\end{eqnarray*}
|
局所不安定性解析
原子弾性剛性係数の成分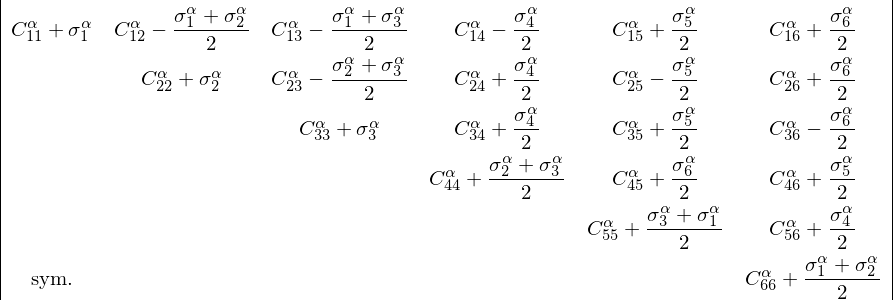
\renewcommand{\arraystretch}{2}
\begin{eqnarray*}
\begin{array}{|cccccc|}
C_{11}^\alpha+\sigma_{1}^\alpha & C_{12}^\alpha-\displaystyle\frac{\sigma_{1}^\alpha+\sigma_{2}^\alpha}{2} &
C_{13}^\alpha-\displaystyle\frac{\sigma_{1}^\alpha+\sigma_{3}^\alpha}{2} &
C_{14}^\alpha-\displaystyle\frac{\sigma_{4}^\alpha}{2} & C_{15}^\alpha+\displaystyle\frac{\sigma_{5}^\alpha}{2} &
C_{16}^\alpha+\displaystyle\frac{\sigma_{6}^\alpha}{2} \\
& C_{22}^\alpha+\sigma_{2}^\alpha & C_{23}^\alpha-\displaystyle\frac{\sigma_{2}^\alpha+\sigma_{3}^\alpha}{2} &
C_{24}^\alpha+\displaystyle\frac{\sigma_{4}^\alpha}{2} & C_{25}^\alpha-\displaystyle\frac{\sigma_{5}^\alpha}{2} &
C_{26}^\alpha+\displaystyle\frac{\sigma_{6}^\alpha}{2} \\
& & C_{33}^\alpha+\sigma_{3}^\alpha & C_{34}^\alpha+\displaystyle\frac{\sigma_{4}^\alpha}{2} &
C_{35}^\alpha+\displaystyle\frac{\sigma_{5}^\alpha}{2} &
C_{36}^\alpha-\displaystyle\frac{\sigma_{6}^\alpha}{2} \\
& & & C_{44}^\alpha+\displaystyle\frac{\sigma_{2}^\alpha+\sigma_{3}^\alpha}{2} &
C_{45}^\alpha+\displaystyle\frac{\sigma_{6}^\alpha}{2} &
C_{46}^\alpha+\displaystyle\frac{\sigma_{5}^\alpha}{2} \\
& & & & C_{55}^\alpha+\displaystyle\frac{\sigma_{3}^\alpha+\sigma_{1}^\alpha}{2} &
C_{56}^\alpha+\displaystyle\frac{\sigma_{4}^\alpha}{2} \\
\mathrm{sym.} & & & & & C_{66}^\alpha+\displaystyle\frac{\sigma_{1}^\alpha+\sigma_{2}^\alpha}{2}\\
\end{array}
\end{eqnarray*}
|