1. �k��SPH�@�Ƃ�
SPH(Smoothed
Particle Hydrodynamics)�@�́C�A���̂̉^����L���̗��q�̉^���Ƃ��āC���U�����闱�q�@�̈��ł���D���l���̉�͎�@�Ƃ��āC���q�@�̂ق��ɁC��Ԃ��i�q�ɂ���ĕ������C���̊i�q�ɕ����ʂ�ϐ��Ƃ��Ċ��蓖�ĂČv�Z����i�q�@���p������D�i�q�@�ł́C�v�Z�̑O�����Ƃ��Ċi�q�̍쐬���K�v�ł��邪�C���q�@�ł͊i�q�̊T�O���Ȃ����ߊi�q�쐬�̂��߂̑O������K�v�Ƃ����C�v�Z�R�X�g��}���邱�Ƃ��ł���D�܂��C�i�q�@�Ɣ�r���ė��q�@�̕����C�_��U�z�≻�w�������m�Ȃǂ̕����̑��������荇�����������̌v�Z���e�Ղł���Ƃ���Ă���D���̂��߁C�{�����ł͗��q�@��p�����D
���q�@�́C�A���̂̉^����L���̗��q�̉^���Ƃ��āC���U�����鐔�l��͎�@�ł���C�v�Z�_(���q)�������ʂƂƂ��Ɉړ����邽�߁C�x�z�����������O�����W���`���ŕ\���Čv�Z���Ă���D���̗��q�@�̈��ł���SPH�@�ł́C���q�����_�ł͂Ȃ��C�e���q�̎��ʂ����q�̈ʒu���\����_�̎���ɂȂ߂炩�ɕ��z����Ƃ��Ă���C���̕��z�͈̔͂����q�̑��ݍ�p�̈�ƂȂ�D���̎��ʂ̍L�����ʂ��āC���q�n�Ɨ��̌n�ŕ����ʂ̑Ή��W���t�����C���̌nNavier-Stokes���������痱�q�n�̉^�����������������DSPH�@�ɂ������b�������̓��o�̉ߒ��͊i�q�@�Ɣ�r���C�����Ȃ��̂ł͂Ȃ��C���Ȃ�̒��x�����I�ł��邪�C����ꂽ�������̓j���[�g���͊w�̉^���������ł���C���̌��ʂ͔��ɂ悭���̂̉^�����Č����Ă���(1)�D
SPH�@�̒��ł��{�����ŗp�����k��SPH�@�ł́C�]���̈��k��SPH�@�ƈقȂ�C�\���q–�C���q�@�ɂ��ƂÂ�������@�ɂ���āC�S����O�͂ɂ��ω����������Ƃ��Ă����x�ψꉻ�������s���C���x����ۂ��C���x����X�V���邱�ƂŁC�k��������ߎ��I�Ɏ������Ă���v�Z��@�ł���(2)�D�k���������߂ɕK�v�ł��閧�x�ψꉻ�ɂ��ẮC�x�z���������v�Z�̎��ԍ���![]() �Ɣ�r���āC�\���ɏ��������ԊԊu�Ŗ��x��
�Ɣ�r���āC�\���ɏ��������ԊԊu�Ŗ��x��![]() �ɑ��Ė��x�ψꉻ���s���D
�ɑ��Ė��x�ψꉻ���s���D
2.
�v�Z��@
�@SPH�@�ɂ����Ċ�b�ƂȂ����x��![]() �́C�J�[�l����
�́C�J�[�l����![]() �ɂ���ĘA���I�Ɏ��ʕ��z���ꂽ���q�̎���
�ɂ���ĘA���I�Ɏ��ʕ��z���ꂽ���q�̎���![]() �̑������킹�ŗ^������D���������āC���闱�q
�̑������킹�ŗ^������D���������āC���闱�q![]() �̈ʒu�ɂ����閧�x
�̈ʒu�ɂ����閧�x![]() �́C���q
�́C���q![]() �𗱎q
�𗱎q![]() �̎��ӗ��q�Ƃ��C���q�ԋ�����
�̎��ӗ��q�Ƃ��C���q�ԋ�����![]() �Ƃ���ƁC�ȉ��̂悤�ɕ\����D
�Ƃ���ƁC�ȉ��̂悤�ɕ\����D
![]()
�Ȃ��C���q�̎���![]() �͋�ԉ𑜃X�P�[��
�͋�ԉ𑜃X�P�[��![]() ��p���āC�}1�̂悤�ȗ��q���z�肵�C�ȉ��̂悤�ɒ�`�ł���D
��p���āC�}1�̂悤�ȗ��q���z�肵�C�ȉ��̂悤�ɒ�`�ł���D
![]()
�{�����ŗp�����J�[�l����![]() �́C���q�ԋ���
�́C���q�ԋ���![]() �Ƌ�ԉ𑜃X�P�[��
�Ƌ�ԉ𑜃X�P�[��![]() �Œ�`����C�W���I�ɗp������M4�X�v���C������p�����D��ԉ𑜃X�P�[��
�Œ�`����C�W���I�ɗp������M4�X�v���C������p�����D��ԉ𑜃X�P�[��![]() �́C���q1�̉e���͈͂̔����̒����ɓ������CM4�X�v���C������p�����J�[�l����
�́C���q1�̉e���͈͂̔����̒����ɓ������CM4�X�v���C������p�����J�[�l����![]() �́C��(13)�Ɏ������q�ԋ���
�́C��(13)�Ɏ������q�ԋ���![]() ����ԉ𑜃X�P�[���ŏ�����������������
����ԉ𑜃X�P�[���ŏ�����������������![]() ��p���āC�ȉ��̂悤�ɕ\����(�}2)�D
��p���āC�ȉ��̂悤�ɕ\����(�}2)�D
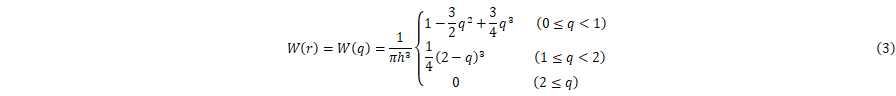
![]()
�{�����ŗp�����x�z�������́C3����Navier-Stokes�������ł���C���̗v�f�̗e�ϕω��������ł����}�b�n���̉�����C���x�C���x�C���ԁC���́C�S�x�C�O�́C���O�����W�������C�i�u�������ꂼ��![]() �C
�C![]() �C
�C![]() �C
�C![]() �C
�C![]() �C
�C![]() �C
�C![]() �C
�C![]() �Ƃ���ƁC���O�����W���`���ňȉ��̂悤�ɕ\����. �܂��C�{�v�Z�Ŏg�p���������l���\16�Ɏ����D
�Ƃ���ƁC���O�����W���`���ňȉ��̂悤�ɕ\����. �܂��C�{�v�Z�Ŏg�p���������l���\16�Ɏ����D
![]()
��(1)�̉��́C���ԍ��ݕ���![]() �Ƃ���ƁC�ȉ��̂悤�Ȑϕ������������D
�Ƃ���ƁC�ȉ��̂悤�Ȑϕ������������D
![]()
�@��(6)�Ŏ������ϕ��������ɂ����鈳�͍�����єS�����́CSPH�ɂ����Ĉȉ��̂悤�ɕ\���ł���D
���͍�
��(6)�̈��͍��́C�ȉ��̂悤�ɏ�����������D
![]()
�����ŁC��(7)�̊e���́C�����̕������SPH�@�ł́C�ȉ��̂悤�ɕ\����(1)�D
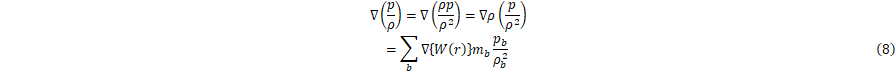
![]()
�@���������āC��(8)����ю�(9)��������Ǝ�(7)�́C�ȉ��̂悤�ɕ\����D
![]()
���̎��C����![]() �͉���
�͉���![]() �̒�`��������x
�̒�`��������x![]() �Ɗ֘A�Â����C�ȉ��̂悤�ɕ\����D
�Ɗ֘A�Â����C�ȉ��̂悤�ɕ\����D
![]()
�@����āC��(11)��������ƁC��(10)�͈ȉ��̂悤�ɕ\����D
![]()
�@�܂��C��(13)�������̕�����藬�̌n�Ɨ��q�n�̐��������l���邱�Ƃɂ��C���q![]() �C
�C![]() ���ڕW���x�ł��镨�����x�����ꂼ��
���ڕW���x�ł��镨�����x�����ꂼ��![]() �C
�C![]() �Ƃ���ƁC�ȉ��̂悤�ɕ\����(1)�D
�Ƃ���ƁC�ȉ��̂悤�ɕ\����(1)�D
![]()
�S����
��(2)�̔S�����́C�����̕������SPH�@�ł́C�ȉ��̂悤�ɕ\����(1)�D
![]()
�@���͍��Ɠ��l�ɁC�����̕�����藬�̌n�Ɨ��q�n�̐��������l���邱�Ƃɂ��C�ȉ��̂悤�ɕ\����(1)�D
![]()
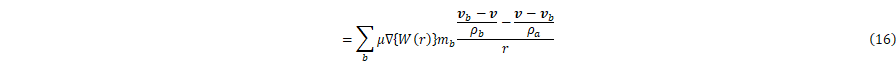
![]()
�\���q–�C���q�@(�}3)
��q�����悤�ɁC�k��SPH�@�ł͏]���̈��k��SPH�@�ƈقȂ�C�\���q–�C���q�@�ɂ��ƂÂ�������@�ɂ���āC�S����O�͂ɂ��ω����������Ƃ��Ă����x�ψꉻ�������s�����ƂŁC���x�ψ�܂�k���������Ă���D�\���q–�C���q�@�ł́C��(2)�Ŏ�����3����Navier-Stokes�������̉������͍��݂̂��c���C�S�����ƊO�͍��͂��ꂼ��ɂ�鑬�x�ω������������\�����x![]() �Ƃ��C�ȉ��̂悤�ɕ\���Ă���D
�Ƃ��C�ȉ��̂悤�ɕ\���Ă���D
![]()
�����ŁC�k���ł��邽�߁C����![]() �ɂ����閧�x��
�ɂ����閧�x��![]() �́C
�́C![]() �ł���D�������C���x��
�ł���D�������C���x��![]() �͗\�����x
�͗\�����x![]() �ɂ���Ă��ꂼ��̗��q���W���ψʂ���Ƌψ�Ȗ��x�ꂪ������D���̎��C�\�����x
�ɂ���Ă��ꂼ��̗��q���W���ψʂ���Ƌψ�Ȗ��x�ꂪ������D���̎��C�\�����x![]() �͉���
�͉���![]() �Ɣ�r�����
�Ɣ�r�����![]() �ł��邽�߁C����
�ł��邽�߁C����![]() �ƌ��т������͂ɂ���Ė��x���z�͊ɘa�Ɍ������D���������āC�v�Z�̎��ԍ���
�ƌ��т������͂ɂ���Ė��x���z�͊ɘa�Ɍ������D���������āC�v�Z�̎��ԍ���![]() �Ɣ�r���āC�\���ɏ��������ԊԊu�Ŗ��x��
�Ɣ�r���āC�\���ɏ��������ԊԊu�Ŗ��x��![]() �ɑ��Ė��x�ψꉻ���s�����ƂŁC���x��͍Ăыψ�ɂȂ�C
�ɑ��Ė��x�ψꉻ���s�����ƂŁC���x��͍Ăыψ�ɂȂ�C![]() �����������Ɠ����ɁC�V���ȑ��x��
�����������Ɠ����ɁC�V���ȑ��x��![]() ��������D
��������D
��̓I�Ȗ��x�ψꉻ��@�Ƃ��ẮC�ȉ��̂Ƃ���ł���D�܂��C���ԍ���![]() �ɑ��ď\�������x�ψꉻ���ԍ��ݕ�
�ɑ��ď\�������x�ψꉻ���ԍ��ݕ�![]() (
(![]() )�ɂ����ĔS������ъO�͂���Z�o�������x(�ȍ~�C���x�\���q)�Ɋ�Â��ė��q�̍��W��ψʂ�����D���̍ۂɐ����鈳�͌��z�ɂ���āC���̑��x�\���q���C�����鑬�x�C���q���Z�o���������ψʂ����{����\���q–�C���q�@�Ɋ�Â�������@��p���āC��(18)�������D
)�ɂ����ĔS������ъO�͂���Z�o�������x(�ȍ~�C���x�\���q)�Ɋ�Â��ė��q�̍��W��ψʂ�����D���̍ۂɐ����鈳�͌��z�ɂ���āC���̑��x�\���q���C�����鑬�x�C���q���Z�o���������ψʂ����{����\���q–�C���q�@�Ɋ�Â�������@��p���āC��(18)�������D
���̎��C���͌��z�͎�(11)�̂悤�ɖ��x���z�Ɗ֘A�t�����邽�߁C���x�ψꉻ�̎��ԍ��ݕ�![]() �͎�(11)��p���āC�ȉ��̂悤�ɕ\����D
�͎�(11)��p���āC�ȉ��̂悤�ɕ\����D
![]()
�����ŁC�\���q–�C���q�@�ŗp���鑬�x�\���q��![]() �C���x�C���q��
�C���x�C���q��![]() �C���x�C���q�Ɋ�Â��ė��q���ړ��������ꍇ�ɂ�����ψʂ�
�C���x�C���q�Ɋ�Â��ė��q���ړ��������ꍇ�ɂ�����ψʂ�![]() �C���x�C���q�Ɋ�Â��ė��q���ړ��������ꍇ�ɂ����鈳�͂̕ω��ʂ�
�C���x�C���q�Ɋ�Â��ė��q���ړ��������ꍇ�ɂ����鈳�͂̕ω��ʂ�![]() �C���x�C���q�Ɋ�Â��ė��q���ړ��������ꍇ�ɂ����閧�x��
�C���x�C���q�Ɋ�Â��ė��q���ړ��������ꍇ�ɂ����閧�x��![]() �Ƃ��C��(19)�Ŏ��������x�ψꉻ�̎��ԍ��ݕ�
�Ƃ��C��(19)�Ŏ��������x�ψꉻ�̎��ԍ��ݕ�![]() ��p����ƁC��(18)�͈ȉ��̂悤�ɏ�����������D
��p����ƁC��(18)�͈ȉ��̂悤�ɏ�����������D
![]()
![]()
![]()
![]()
�@�����ŁC��(13)��������Ǝ�(23)�́C�v�Z�̑ΏۂƂ��闱�q![]() �̑��x��
�̑��x��![]() �Ƃ���ƁC�ȉ��̂悤�ɕ\����D
�Ƃ���ƁC�ȉ��̂悤�ɕ\����D
![]()
�{�����ł́C�����̕����ɂ�����肵���v�Z���s�����߂̕��@���̗p���C���q�̌v�Z���x�����̗��q�̖ڕW���x�i�������x�j����������炻�̍���0�Ƃ��Čv�Z���Ȃ����ƂƂ����D���x�����ۂ̒l���傫���Ȃ������q�̉e���͎邱�Ƃ��ł���̂ŁC�����I�Ȗ��x�ψꉻ����Ɏx��͏o�Ȃ�(1)�D�ɓ��̌����ɂ��ƁC���̖��x���ɂ����āC�����𑝂₵������Ɛ��l�g�U�ɂ��v�Z��̔S�������傷��X��������C�t�ɔ��������炵������Ɩ��x�ꂪ�����l���瘨�����邽�߁C�J���}���Q����Č������\���������C������1��Ƃ���(2)�D�܂��C��(23)�œ����鑬�x![]() �Ɏ�(1)�̔S�����ƊO�͍������������̂��C�������̑��x�C���q�̏����l�C���Ȃ킿�\���q�ƂȂ�C�ȉ��̂悤�ɕ\����D
�Ɏ�(1)�̔S�����ƊO�͍������������̂��C�������̑��x�C���q�̏����l�C���Ȃ킿�\���q�ƂȂ�C�ȉ��̂悤�ɕ\����D
![]()
����ɂ��C1�̌v�Z�X�e�b�v�I�����C���̌v�Z�X�e�b�v�Ɉڂ�D���̌v�Z�̗����}4�ɂ܂Ƃ߂��D
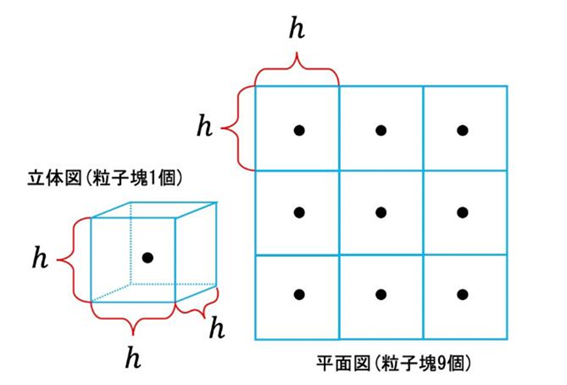
�}1�@���q��
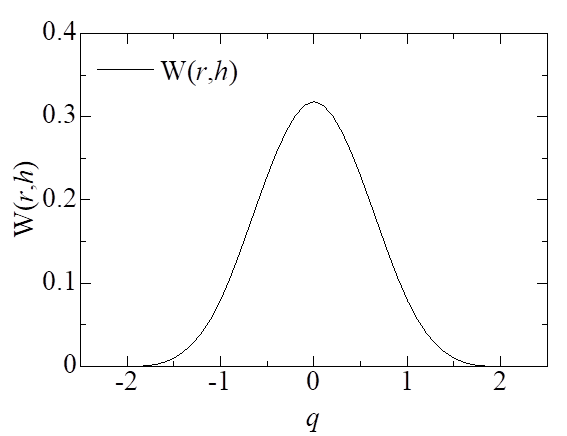
�}2�@�J�[�l����
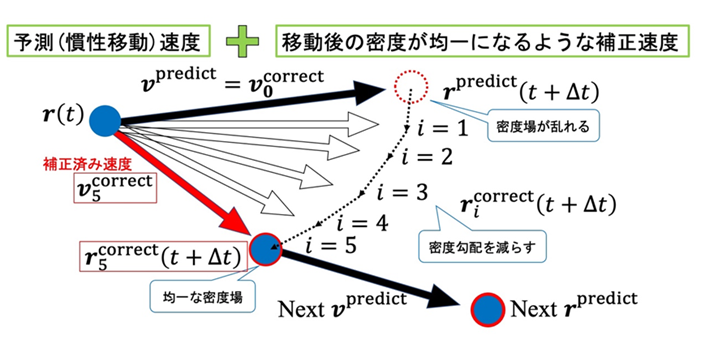
�}3�@�\���q-�C���q�@
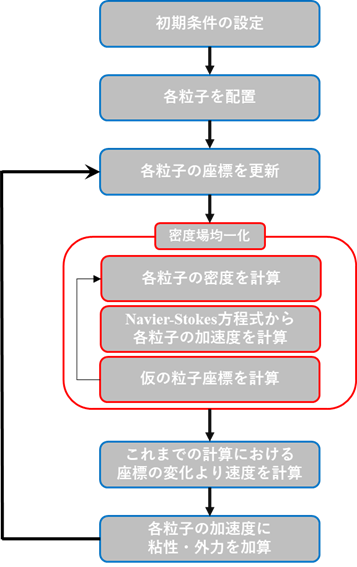
�}4�@�kSPH�@�ɂ�����v�Z�t���[�`���[�g
�ȒP��SPH�@�ɂ��ĉ���������C�ȉ��̘_�����Q�l�ɂ���,��ǂ��������߂���D��ts-kikuchilab���ɕۑ��ς�
(2)
�ɓ��^��, �g�k��SPH�@��p�����A�[�N�n�ڃv���Z�X���������ۂ̐��l�V�~�����[�V�����h, ���k��w��w�@�H�w�����ȋ@�B�V�X�e���f�U�C���H�w��U 2015�N�x���m�w�ʘ_��, 2016
(3)
Manuel Hirschler, Ulrich Nieken, �eStudy
of implicit time-integration in truly incompressible SPH�f, SPHERIC, 2017
3. �v�Z�R�[�h
�E��`
|
#define
NMAX
(300) #define
DT
(5.0e-4f) #define
P_SPACING (5.0e-4f) #define
H P_SPACING #define
A0 0.004f #define
B0 0.002f #define
AB 0.0045f #define
RHO_WATER 1000.0f #define
M_WATER (RHO_WATER
* P_SPACING * P_SPACING * P_SPACING) #define
C_WATER (1.453e3f) #define
NU_WATER (1.0038e-6f)
#define
DAMPING_STEP (P_SPACING
/ C_WATER) //3.441156*10^-7 #define
DAMPLMT
5 #define
BG 0.994f #define
SURFACE_MACRO
72.75e-3f #define
GAMMA (
SURFACE_MACRO * P_SPACING / M_WATER ) |
|
NMAX |
�v�Z�� |
|
DT |
���ԊԊu |
|
P_SPACING |
�ׂ荇�����q�Ƃ̋���(���S�ƒ��S) |
|
H |
��ԉ𑜃X�P�[�� |
|
A0,B0 |
���q��z�u����ȉ~�̑傫�� |
|
AB |
�v�Z�ɂ����錴�_�ƕ\���̌��_�̒��� |
|
RHO_WATER |
���̖��x |
|
M_WATER |
�����q1���̎��� |
|
C_WATER |
���̉��� |
|
NU_WATER |
���̓��S�x |
|
DAMPING_STEP |
����c�Ƌ�ԉ𑜃X�P�[��h�Ɉˑ����閧�x�ψꉻ���ԍ��ݕ���t�f=h/c(<<��t) |
|
DAMPLMT |
���x�ψꉻ�̂��߂̔����� |
|
BG |
�ڕW���x�ƌv�Z���x������ɂȂ�Ȃ����߂̕�W�� |
|
SURFACE_MACRO |
20���̐��̕\�ʒ��� [N/m] |
|
GAMMA |
���q�����\�ʒ��� [m/s^2] |
|
EQT |
�\�ʒ��͋ψꉻ�̂��߂̔����� |
�E���q���̌v�Z(void
set_particle_number)
|
void
set_particle_number() { float
a0 = A0, b0 = B0, caldl = 0.0f; int
is = (int) (a0 * 2.0f / (float) H) + 1, js = (int) (b0 * 2.0f / (float) H) +
1, ks = (int) (b0 * 2.0f / (float) H) + 1; float
inix = -a0 + (float) H * 0.5f, iniy = -b0 + (float) H * 0.5f, iniz = -b0 +
(float) H * 0.5f; float
x0, y0, z0; for
(int k = 0; k < ks; k++) { z0
= iniz + (float) k * (float) H; for
(int j = 0; j < js; j++) { y0
= iniy + (float) j * (float) H; for
(int i = 0; i < is; i++) { x0
= inix + (float) i * (float) H; caldl
= x0 * x0 / a0 / a0 + y0 * y0 / b0 / b0 + z0 * z0 / b0 / b0; if
(caldl < 1.0f) { np++; } } } } cout
<< "The number of water particles : " << np <<
endl; } |
�����ł́C�w�肵���͈͓�(�{�v�Z�ł�A0�EB0��萔�Ƃ����ȉ~��)�ɗׂ荇�����q�Ƃ̋���(���q�̑傫��)P_SPACING(H)[mm]�ŁA�����z�u�ł��邩�v�Z����D
�E���q�̔z�u(void set_particle)
|
void
set_particle(float xp[], float yp[], float zp[], float up[], float vp[],
float wp[], float dp[]) { float
a0 = A0, b0 = B0, caldl = 0.0f; int
is = (int) (a0 * 2.0f / (float) H) + 1, js = (int) (b0 * 2.0f / (float) H) +
1, ks = (int) (b0 * 2.0f / (float) H) + 1; float
inix = -a0 + (float) H * 0.5f, iniy = -b0 + (float) H * 0.5f, iniz = -b0 +
(float) H * 0.5f; float
x0, y0, z0; np
= 0; for
(int k = 0; k < ks; k++) { z0
= iniz + (float) k * (float) H; for
(int j = 0; j < js; j++) { y0
= iniy + (float) j * (float) H; for
(int i = 0; i < is; i++) { x0
= inix + (float) i * (float) H; caldl
= x0 * x0 / a0 / a0 + y0 * y0 / b0 / b0 + z0 * z0 / b0 / b0; if
(caldl < 1.0f) { xp[np]
= x0 + AB; yp[np]
= y0 + AB; zp[np]
= z0 + AB; up[np]
= 0.0f; vp[np]
= 0.0f; wp[np]
= 0.0f; dp[np]
= (float) RHO_WATER; np++; } } } } } |
��قnjv�Z�����͈͓��ɔz�u�ł��闱�q�����ő�l�Ƃ��āC���q�����ۂɔz�u���C���ꂼ��ɔԍ���U��D�܂��CAB�ɂ���Čv�Z�ɂ����錴�_�ƕ\���̌��_�̒������Ă���D
void
gnuplot_location�͏ȗ�
�E���q�̈ړ� (void realmove)
|
void
realmove(float xp[], float yp[], float zp[], float xpp[], float ypp[], float
zpp[], float up[], float vp[], float wp[], unsigned int np0) { for
(unsigned int i = 0; i < np0; i++) { xp[i]
= xpp[i] + up[i] * DT; yp[i]
= ypp[i] + vp[i] * DT; zp[i]
= zpp[i] + wp[i] * DT; } } |
���q�̍��W�x�Ǝ��ԕω��ɂ���Ĉړ������Ă���(![]() )�D�����l�ɂ��Ă�[void set_particle] �ɂĂ��ꂼ��0�ƂȂ��Ă���D
)�D�����l�ɂ��Ă�[void set_particle] �ɂĂ��ꂼ��0�ƂȂ��Ă���D
�E���x�̌v�Z(void getDensity)
|
void
getDensity(float dp[], float xp[], float yp[], float zp[], unsigned int np0)
{ float
disx, disy, disz, dis, q, kernel, densityTemp, divH = 1.0f / H, c1 = divH *
divH * divH / M_PI, mass = M_WATER; for
(unsigned int i = 0; i < np0; i++) { densityTemp
= 0.0f; for
(unsigned int j = 0; j < np0; j++) { disx
= xp[j] - xp[i]; disy
= yp[j] - yp[i]; disz
= zp[j] - zp[i]; dis
= sqrtf(disx * disx + disy * disy + disz * disz); q
= dis * divH; if
(q < 2.0f) { if
(q < 1.0f) kernel
= c1 * (1.0f - 1.5f * q * q + 0.75f * q * q * q); else kernel
= c1 * (2.0f - 3.0f * q + 1.5f * q * q - 0.25f * q * q * q); densityTemp
+= mass * kernel; } } dp[i]
= densityTemp; } } |
�@
�@�����ł́C�Ώۗ��q�̖��x�𑼂̗��q�Ƃ̉e���ɂ���Čv�Z���Ă���D
�E�����x�̌v�Z(void getAcceleration)
|
void
getAcceleration(float axp[], float ayp[], float azp[], float dp[], float xp[],
float yp[], float zp[], unsigned int np0) { float
disx, disy, disz, dis, q, der_k, accelX, accelY, accelZ, ap, divDis; float
divH = 1.0f / H, c1 = divH * divH * divH / M_PI, mc2 = M_WATER * C_WATER *
C_WATER, bgt = BG * RHO_WATER; for
(unsigned int i = 0; i < np0; i++) { accelX
= 0.0f; accelY
= 0.0f; accelZ
= 0.0f; for
(unsigned int j = 0; j < np0; j++) { if
(j != i) { disx
= xp[j] - xp[i]; disy
= yp[j] - yp[i]; disz
= zp[j] - zp[i]; dis
= sqrtf(disx * disx + disy * disy + disz * disz); divDis
= 1.0f / dis; q
= dis * divH; if
(q < 2.0f) { if
(q < 1.0f) der_k
= c1 * (-3.0f * q + 2.25f * q * q) * divH; else der_k
= c1 * (-3.0f + 3.0f * q - 0.75f * q * q) * divH; ap
= mc2 * ((dp[i] - bgt) / (dp[i] * dp[i]) + (dp[j] - bgt) / (dp[j] * dp[j])) *
divDis * der_k; accelX
+= ap * disx; accelY
+= ap * disy; accelZ
+= ap * disz; } } } axp[i]
= accelX; ayp[i]
= accelY; azp[i]
= accelZ; } } |
�@�����ł́C�Ώۗ��q�̉����x��Navier-Stokes�������̈��͍��ɂ���Čv�Z���Ă���D
�E���̗��q���W�̌v�Z(void imgMove)
|
void
imgMove(float axp[], float ayp[], float azp[], float xp[], float yp[], float
zp[], unsigned int np0) { float
timeStep = DAMPING_STEP; float
temp; temp
= 0.5f * timeStep * timeStep; for
(unsigned int i = 0; i < np0; i++) { xp[i]
+= axp[i] * temp; yp[i]
+= ayp[i] * temp; zp[i]
+= azp[i] * temp; } } |
�@�����ł́C�Ώۗ��q���������x�ɑ���ړ������ł���B���x���̂��ߔ�������̂ʼn��̈ړ��ł���D����![]() �Ƌ�ԉ𑜃X�P�[��
�Ƌ�ԉ𑜃X�P�[��![]() �Ɉˑ����閧�x�ψꉻ���ԍ��ݕ�
�Ɉˑ����閧�x�ψꉻ���ԍ��ݕ�![]() �����ԍ��݂ŁC
�����ԍ��݂ŁC![]() �����ԍ��݂łȂ����Ƃɒ��ӁD
�����ԍ��݂łȂ����Ƃɒ��ӁD
�ugetDensity�AgetAcceleration�AimgMove�v���J��Ԃ��D
![]()
�E�\�ʒ���(void surfaceAttraction)
|
void
surfaceAttraction(float axsp[], float aysp[], float azsp[], float xp[], float
yp[], float zp[], unsigned int np0) { float
disx, disy, disz, dis, q, kernel, accelX, accelY, accelZ, temp; float
divH = 1.0f / H, c1 = divH * divH * divH / M_PI, gamma = GAMMA; for
(unsigned int i = 0; i < np0; i++) { accelX
= 0.0f; accelY
= 0.0f; accelZ
= 0.0f; for
(unsigned int j = 0; j < np0; j++) { if
(j != i) { disx
= xp[j] - xp[i]; disy
= yp[j] - yp[i]; disz
= zp[j] - zp[i]; dis
= sqrtf(disx * disx + disy * disy + disz * disz); q
= dis * divH; if
(q < 2.0f) { if
(q < 1.0f) kernel
= q; else kernel
= 2.0f - q; temp
= gamma * kernel / dis; accelX
+= temp * disx; accelY
+= temp * disy; accelZ
+= temp * disz; } } } axsp[i]
= accelX; aysp[i]
= accelY; azsp[i]
= accelZ; } } |
�@
�@�����ł́C�v�Z���q�����\�ʒ��͂�l�H���͂Ƃ��Čv�Z���Ă���B
�E�\�ʒ��͂̕��ω�(void aspSmoothing)
|
void
aspSmoothing(float axsp[], float aysp[], float azsp[], float axp[], float
ayp[], float azp[], float xp[], float yp[], float zp[], unsigned int np0) { float
disx, disy, disz, dis, q, kernel, accelX, accelY, accelZ, weight, divWeight; float
divH = 1.0f / H, c1 = divH * divH * divH / M_PI; for
(unsigned int i = 0; i < np0; i++) { accelX
= axsp[i] * c1; accelY
= aysp[i] * c1; accelZ
= azsp[i] * c1; weight
= c1; for
(unsigned int j = 0; j < np0; j++) { if
(j != i) { disx
= xp[j] - xp[i]; disy
= yp[j] - yp[i]; disz
= zp[j] - zp[i]; dis
= sqrtf(disx * disx + disy * disy + disz * disz); q
= dis * divH; if
(q < 2.0f) { if
(q < 1.0f) kernel
= c1 * (1.0f - 1.5f * q * q + 0.75f * q * q * q); else kernel
= c1 * (2.0f - 3.0f * q + 1.5f * q * q - 0.25f * q * q * q); accelX
+= axsp[j] * kernel; accelY
+= aysp[j] * kernel; accelZ
+= azsp[j] * kernel; weight
+= kernel; } } } divWeight
= 1.0f / weight; axp[i]
= accelX * divWeight; ayp[i]
= accelY * divWeight; azp[i]
= accelZ * divWeight; } } |
�����ł́C�d�݊�(�J�[�l����)��p���Čv�Z���q�Ƃ��̎��ӗ��q�����\�ʒ���(�l�H����)�ω����Ă���D
�E�\�ʒ��͂ɂ��ړ�(void surfaceMove)
|
void
surfaceMove(float axsp[], float aysp[], float azsp[], float xp[], float yp[],
float zp[], unsigned int np0) { float
temp; temp
= 0.5f * DT * DT; for
(unsigned int i = 0; i < np0; i++) { xp[i]
+= axsp[i] * temp; yp[i]
+= aysp[i] * temp; zp[i]
+= azsp[i] * temp; } } |
�@�����ł́C���ω����ꂽ�\�ʒ���(�l�H����)���v�Z���q���ړ������Ă���D
�E���x�̌v�Z(void velocityStep)
|
void
velocityStep(float xp[], float yp[], float zp[], float xpp[], float ypp[],
float zpp[], float up[], float vp[], float wp[], unsigned int np0) { float
divDT; divDT
= 1.0f / DT; for
(unsigned int i = 0; i < np0; i++) { up[i]
= (xp[i] - xpp[i]) * divDT; vp[i]
= (yp[i] - ypp[i]) * divDT; // - G_DIRECT*DT; wp[i]
= (zp[i] - zpp[i]) * divDT; } } |
�@�����ł́C�ړ��������������ƂɌv�Z���q�̑��x���v�Z���Ă���D
�E�S���̌v�Z(void viscosity)
|
void
viscosity(float xp[], float yp[], float zp[], float up[], float vp[], float
wp[], float axp[], float ayp[], float azp[], float dp[], unsigned int np0) { float
disx, disy, disz, dis, q, der_k, ut1, vt1, wt1, temp; float
divH = 1.0f / H, c1 = divH * divH * divH / M_PI, nu = NU_WATER; for
(unsigned int i = 0; i < np0; i++) { ut1
= 0.0f; vt1
= 0.0f; wt1
= 0.0f; for
(unsigned int j = 0; j < np0; j++) { if
(j != i) { disx
= xp[j] - xp[i]; disy
= yp[j] - yp[i]; disz
= zp[j] - zp[i]; dis
= sqrtf(disx * disx + disy * disy + disz * disz); q
= dis * divH; if
(q < 2.0f) { if
(q < 1.0f) der_k
= c1 * (-3.0f * q + 2.25f * q * q) * divH; else der_k
= c1 * (-3.0f + 3.0f * q - 0.75f * q * q) * divH; temp
= (dp[i] + dp[j]) * der_k / (dp[i] * dp[j] * dis); ut1
-= temp * (up[j] - up[i]); vt1
-= temp * (vp[j] - vp[i]); wt1
-= temp * (wp[j] - wp[i]); } } } temp
= M_WATER * nu * DT; axp[i]
= up[i] + temp * ut1; ayp[i]
= vp[i] + temp * vt1; azp[i]
= wp[i] + temp * wt1; } } |
�@�����ł́C�S�����v�Z���C�v�Z���q���������x�ɉ��Z���Ă���D
�E�v���O�����̑S�e
�i���jwindows�̐ݒ��u�_(���p)�v���u\�v�ɒu��������Ă���ꍇ������B
|
#include <iostream> #include <fstream> #include <cmath> #include <time.h> #include <string.h> #include <stdlib.h> #include <stdio.h> #include <sys/stat.h> #include <sys/types.h> using namespace std; #define NMAX (300) #define DT
(5.0e-4f) #define P_SPACING (5.0e-4f) #define H P_SPACING #define A0 0.004f #define B0 0.002f #define AB 0.0045f #define RHO_WATER 1000.0f #define M_WATER (RHO_WATER
* P_SPACING * P_SPACING * P_SPACING) /* mass for water particle */ #define C_WATER (1.453e3f) // sonic speed in water #define NU_WATER (1.0038e-6f)
// kinematic viscosity #define DAMPING_STEP (P_SPACING / C_WATER) #define DAMPLMT 5 #define BG 0.994f #define SURFACE_MACRO 72.75e-3f//�i20����
72.75e-3[N/m]�j #define GAMMA (
SURFACE_MACRO * P_SPACING / M_WATER ) //[m/s^2] unsigned int n = 0, np = 0; void set_particle_number() { float
a0 = A0, b0 = B0, caldl = 0.0f; int
is = (int)(a0 * 2.0f / (float)H) + 1, js = (int)(b0 * 2.0f / (float)H) + 1,
ks = (int)(b0 * 2.0f / (float)H) + 1; float
inix = -a0 + (float)H * 0.5f, iniy = -b0 + (float)H * 0.5f, iniz = -b0 +
(float)H * 0.5f; float
x0, y0, z0; for
(int k = 0; k < ks; k++) { z0
= iniz + (float)k * (float)H; for
(int j = 0; j < js; j++) { y0
= iniy + (float)j * (float)H; for
(int i = 0; i < is; i++) { x0
= inix + (float)i * (float)H; caldl
= x0 * x0 / a0 / a0 + y0 * y0 / b0 / b0 + z0 * z0 / b0 / b0; if
(caldl < 1.0f) { np++; } } } } cout
<< "The number of water particles : " << np <<
endl; cout
<< "The number of calculation : " << NMAX <<
endl; } void set_particle(float xp[], float
yp[], float zp[], float up[], float vp[], float wp[], float dp[]) { float
a0 = A0, b0 = B0, caldl = 0.0f; int
is = (int)(a0 * 2.0f / (float)H) + 1, js = (int)(b0 * 2.0f / (float)H) + 1,
ks = (int)(b0 * 2.0f / (float)H) + 1; float
inix = -a0 + (float)H * 0.5f, iniy = -b0 + (float)H * 0.5f, iniz = -b0 +
(float)H * 0.5f; float
x0, y0, z0; np
= 0; for
(int k = 0; k < ks; k++) { z0
= iniz + (float)k * (float)H; for
(int j = 0; j < js; j++) { y0
= iniy + (float)j * (float)H; for
(int i = 0; i < is; i++) { x0
= inix + (float)i * (float)H; caldl
= x0 * x0 / a0 / a0 + y0 * y0 / b0 / b0 + z0 * z0 / b0 / b0; if
(caldl < 1.0f) { xp[np]
= x0 + AB; yp[np]
= y0 + AB; zp[np]
= z0 + AB; up[np]
= 0.0f; vp[np]
= 0.0f; wp[np]
= 0.0f; dp[np]
= (float)RHO_WATER; np++; } } } } } void gnuplot_location(float xp[], float
yp[], float zp[]) { char
str2[20]; sprintf(str2,
"./img"); mkdir(str2,
0755); sprintf(str2,
"./img/location"); mkdir(str2,
0755); FILE*
gp; gp
= popen("gnuplot", "w"); fprintf(gp,
"set terminal png font \"Times,45\" size 1920,1080\n"); fprintf(gp,
"set border lw 5.0\n"); fprintf(gp,
"set ticscale 0.8\n"); fprintf(gp,
"set ylabel \"{/Times-Italic y} [mm]\" rotate by 90 offset
0.0,0\n"); fprintf(gp,
"set xlabel \"{/Times-Italic x} [mm]\" offset 0,0.0\n"); fprintf(gp,
"set xrange[-0.0045:0.0045]\n"); fprintf(gp,
"set yrange[-0.0045:0.0045]\n"); fprintf(gp,
"set zrange[-0.0045:0.0045]\n"); fprintf(gp,
"set xtics (\"-4\" -0.004, \"-3\" -0.003,
\"-2\" -0.002, \"-1\" -0.001, \"0\" 0,
\"4\" 0.004, \"3\" 0.003, \"2\" 0.002,
\"1\" 0.001,)\n"); fprintf(gp,
"set ytics (\"-4\" -0.004, \"-3\" -0.003,
\"-2\" -0.002, \"-1\" -0.001, \"0\" 0,
\"4\" 0.004, \"3\" 0.003, \"2\" 0.002,
\"1\" 0.001,)\n"); fprintf(gp,
"set ztics (\"-4\" -0.004, \"-3\" -0.003,
\"-2\" -0.002, \"-1\" -0.001, \"0\" 0,
\"4\" 0.004, \"3\" 0.003, \"2\" 0.002,
\"1\" 0.001,)\n"); fprintf(gp,
"set size ratio 1.0\n"); fprintf(gp,
"set nokey\n"); fprintf(gp,
"set view map\n"); fprintf(gp,
"set output \"%s/png%d.png\"\n", str2, n); fprintf(gp,
"splot \"-\" u 1:2:3 with points pt 7 ps 3 lc rgb
\"blue\"\n"); for
(int i = 0; i < np; i++) { fprintf(gp,
"%lf, %lf, %lf\n", xp[i] - AB, yp[i] - AB, zp[i] - AB); } fprintf(gp,
"e\n"); fflush(gp); pclose(gp); } void realmove(float xp[], float yp[],
float zp[], float xpp[], float ypp[], float zpp[], float up[], float vp[],
float wp[], unsigned int np0) { for
(unsigned int i = 0; i < np0; i++) { xp[i]
= xpp[i] + up[i] * DT; yp[i]
= ypp[i] + vp[i] * DT; zp[i]
= zpp[i] + wp[i] * DT; } } void getDensity(float dp[], float xp[],
float yp[], float zp[], unsigned int np0) { float
disx, disy, disz, dis, q, kernel, densityTemp, divH = 1.0f / H, c1 = divH *
divH * divH / M_PI, mass = M_WATER; for
(unsigned int i = 0; i < np0; i++) { densityTemp
= 0.0f; for
(unsigned int j = 0; j < np0; j++) { disx
= xp[j] - xp[i]; disy
= yp[j] - yp[i]; disz
= zp[j] - zp[i]; dis
= sqrtf(disx * disx + disy * disy + disz * disz); q
= dis * divH; if
(q < 2.0f) { if
(q < 1.0f) kernel
= c1 * (1.0f - 1.5f * q * q + 0.75f * q * q * q); else kernel
= c1 * (2.0f - 3.0f * q + 1.5f * q * q - 0.25f * q * q * q); densityTemp
+= mass * kernel; } } dp[i]
= densityTemp; } } void getAcceleration(float axp[], float
ayp[], float azp[], float dp[], float xp[], float yp[], float zp[], unsigned
int np0) { float
disx, disy, disz, dis, q, der_k, accelX, accelY, accelZ, ap, divDis; float
divH = 1.0f / H, c1 = divH * divH * divH / M_PI, mc2 = M_WATER * C_WATER *
C_WATER, bgt = BG * RHO_WATER; for
(unsigned int i = 0; i < np0; i++) { accelX
= 0.0f; accelY
= 0.0f; accelZ
= 0.0f; for
(unsigned int j = 0; j < np0; j++) { if
(j != i) { disx
= xp[j] - xp[i]; disy
= yp[j] - yp[i]; disz
= zp[j] - zp[i]; dis
= sqrtf(disx * disx + disy * disy + disz * disz); divDis
= 1.0f / dis; q
= dis * divH; if
(q < 2.0f) { if
(q < 1.0f) der_k
= c1 * (-3.0f * q + 2.25f * q * q) * divH; else der_k
= c1 * (-3.0f + 3.0f * q - 0.75f * q * q) * divH; ap
= mc2 * ((dp[i] - bgt) / (dp[i] * dp[i]) + (dp[j] - bgt) / (dp[j] * dp[j])) *
divDis * der_k; accelX
+= ap * disx; accelY
+= ap * disy; accelZ
+= ap * disz; } } } axp[i]
= accelX; ayp[i]
= accelY; azp[i]
= accelZ; } } void imgMove(float axp[], float ayp[],
float azp[], float xp[], float yp[], float zp[], unsigned int np0) { float
timeStep = DAMPING_STEP; float
temp; temp
= 0.5f * timeStep * timeStep; for
(unsigned int i = 0; i < np0; i++) { xp[i]
+= axp[i] * temp; yp[i]
+= ayp[i] * temp; zp[i]
+= azp[i] * temp; } } void surfaceAttraction(float axsp[],
float aysp[], float azsp[], float xp[], float yp[], float zp[], unsigned int
np0) { float
disx, disy, disz, dis, q, kernel, accelX, accelY, accelZ, temp; float
divH = 1.0f / H, c1 = divH * divH * divH / M_PI, gamma = GAMMA; for
(unsigned int i = 0; i < np0; i++) { accelX
= 0.0f; accelY
= 0.0f; accelZ
= 0.0f; for
(unsigned int j = 0; j < np0; j++) { if
(j != i) { disx
= xp[j] - xp[i]; disy
= yp[j] - yp[i]; disz
= zp[j] - zp[i]; dis
= sqrtf(disx * disx + disy * disy + disz * disz); q
= dis * divH; if
(q < 2.0f) { if
(q < 1.0f) kernel
= q; else kernel
= 2.0f - q; temp
= gamma * kernel / dis; accelX
+= temp * disx; accelY
+= temp * disy; accelZ
+= temp * disz; } } } axsp[i]
= accelX; aysp[i]
= accelY; azsp[i]
= accelZ; } } void aspSmoothing(float axsp[], float
aysp[], float azsp[], float axp[], float ayp[], float azp[], float xp[],
float yp[], float zp[], unsigned int np0) { float
disx, disy, disz, dis, q, kernel, accelX, accelY, accelZ, weight, divWeight; float
divH = 1.0f / H, c1 = divH * divH * divH / M_PI; for
(unsigned int i = 0; i < np0; i++) { accelX
= axsp[i] * c1; accelY
= aysp[i] * c1; accelZ
= azsp[i] * c1; weight
= c1; for
(unsigned int j = 0; j < np0; j++) { if
(j != i) { disx
= xp[j] - xp[i]; disy
= yp[j] - yp[i]; disz
= zp[j] - zp[i]; dis
= sqrtf(disx * disx + disy * disy + disz * disz); q
= dis * divH; if
(q < 2.0f) { if
(q < 1.0f) kernel
= c1 * (1.0f - 1.5f * q * q + 0.75f * q * q * q); else kernel
= c1 * (2.0f - 3.0f * q + 1.5f * q * q - 0.25f * q * q * q); accelX
+= axsp[j] * kernel; accelY
+= aysp[j] * kernel; accelZ
+= azsp[j] * kernel; weight
+= kernel; } } } divWeight
= 1.0f / weight; axp[i]
= accelX * divWeight; ayp[i]
= accelY * divWeight; azp[i]
= accelZ * divWeight; } } void surfaceMove(float axsp[], float
aysp[], float azsp[], float xp[], float yp[], float zp[], unsigned int np0) { float
temp; temp
= 0.5f * DT * DT; for
(unsigned int i = 0; i < np0; i++) { xp[i]
+= axsp[i] * temp; yp[i]
+= aysp[i] * temp; zp[i]
+= azsp[i] * temp; } } void velocityStep(float xp[], float
yp[], float zp[], float xpp[], float ypp[], float zpp[], float up[], float
vp[], float wp[], unsigned int np0) { float
divDT; divDT
= 1.0f / DT; for
(unsigned int i = 0; i < np0; i++) { up[i]
= (xp[i] - xpp[i]) * divDT; vp[i]
= (yp[i] - ypp[i]) * divDT; // - G_DIRECT*DT; wp[i]
= (zp[i] - zpp[i]) * divDT; } } void viscosity(float xp[], float yp[],
float zp[], float up[], float vp[], float wp[], float axp[], float ayp[],
float azp[], float dp[], unsigned int np0) { float
disx, disy, disz, dis, q, der_k, ut1, vt1, wt1, temp; float
divH = 1.0f / H, c1 = divH * divH * divH / M_PI, nu = NU_WATER; for
(unsigned int i = 0; i < np0; i++) { ut1
= 0.0f; vt1
= 0.0f; wt1
= 0.0f; for
(unsigned int j = 0; j < np0; j++) { if
(j != i) { disx
= xp[j] - xp[i]; disy
= yp[j] - yp[i]; disz
= zp[j] - zp[i]; dis
= sqrtf(disx * disx + disy * disy + disz * disz); q
= dis * divH; if
(q < 2.0f) { if
(q < 1.0f) der_k
= c1 * (-3.0f * q + 2.25f * q * q) * divH; else der_k
= c1 * (-3.0f + 3.0f * q - 0.75f * q * q) * divH; temp
= (dp[i] + dp[j]) * der_k / (dp[i] * dp[j] * dis); ut1
-= temp * (up[j] - up[i]); vt1
-= temp * (vp[j] - vp[i]); wt1
-= temp * (wp[j] - wp[i]); } } } temp
= M_WATER * nu * DT; axp[i]
= up[i] + temp * ut1; ayp[i]
= vp[i] + temp * vt1; azp[i]
= wp[i] + temp * wt1; } } int main() { set_particle_number(); float*
h_xp, * h_yp, * h_zp, * h_up, * h_vp, * h_wp, * h_dp, * h_xpp, * h_ypp, *
h_zpp, * h_axp, * h_ayp, * h_azp, * h_axsp, * h_aysp, * h_azsp; h_xp
= (float*)malloc(np * sizeof(float)); h_yp
= (float*)malloc(np * sizeof(float)); h_zp
= (float*)malloc(np * sizeof(float)); h_up
= (float*)malloc(np * sizeof(float)); h_vp
= (float*)malloc(np * sizeof(float)); h_wp
= (float*)malloc(np * sizeof(float)); h_dp
= (float*)malloc(np * sizeof(float)); h_xpp
= (float*)malloc(np * sizeof(float)); h_ypp
= (float*)malloc(np * sizeof(float)); h_zpp
= (float*)malloc(np * sizeof(float)); h_axp
= (float*)malloc(np * sizeof(float)); h_ayp
= (float*)malloc(np * sizeof(float)); h_azp
= (float*)malloc(np * sizeof(float)); h_axsp
= (float*)malloc(np * sizeof(float)); h_aysp
= (float*)malloc(np * sizeof(float)); h_azsp
= (float*)malloc(np * sizeof(float)); memset(h_xp,
0, np * sizeof(float)); memset(h_yp,
0, np * sizeof(float)); memset(h_zp,
0, np * sizeof(float)); memset(h_up,
0, np * sizeof(float)); memset(h_vp,
0, np * sizeof(float)); memset(h_wp,
0, np * sizeof(float)); memset(h_dp,
0, np * sizeof(float)); memset(h_xpp,
0, np * sizeof(float)); memset(h_ypp,
0, np * sizeof(float)); memset(h_zpp,
0, np * sizeof(float)); memset(h_axp,
0, np * sizeof(float)); memset(h_ayp,
0, np * sizeof(float)); memset(h_azp,
0, np * sizeof(float)); memset(h_axsp,
0, np * sizeof(float)); memset(h_aysp,
0, np * sizeof(float)); memset(h_azsp,
0, np * sizeof(float)); set_particle(h_xp,
h_yp, h_zp, h_up, h_vp, h_wp, h_dp); gnuplot_location(h_xp,
h_yp, h_zp); for
(n = 1; n < NMAX + 1; n++) { memcpy(h_xpp,
h_xp, np * sizeof(float)); memcpy(h_ypp,
h_yp, np * sizeof(float)); memcpy(h_zpp,
h_zp, np * sizeof(float)); realmove(h_xp,
h_yp, h_zp, h_xpp, h_ypp, h_zpp, h_up, h_vp, h_wp, np); for
(int loop0 = 0; loop0 < DAMPLMT;
loop0++) { getDensity(h_dp,
h_xp, h_yp, h_zp, np); getAcceleration(h_axp,
h_ayp, h_azp, h_dp, h_xp, h_yp, h_zp, np); imgMove(h_axp,
h_ayp, h_azp, h_xp, h_yp, h_zp, np); } surfaceAttraction(h_axsp,
h_aysp, h_azsp, h_xp, h_yp, h_zp, np); for
(int loop0 = 0; loop0 < 3; loop0++) { aspSmoothing(h_axsp,
h_aysp, h_azsp, h_axp, h_ayp, h_azp, h_xp, h_yp, h_zp, np); memcpy(h_axsp,
h_axp, np * sizeof(float)); memcpy(h_aysp,
h_ayp, np * sizeof(float)); memcpy(h_azsp,
h_azp, np * sizeof(float)); } surfaceMove(h_axsp,
h_aysp, h_azsp, h_xp, h_yp, h_zp, np); gnuplot_location(h_xp,
h_yp, h_zp); velocityStep(h_xp,
h_yp, h_zp, h_xpp, h_ypp, h_zpp, h_up, h_vp, h_wp, np); viscosity(h_xp,
h_yp, h_zp, h_up, h_vp, h_wp, h_axp, h_ayp, h_azp, h_dp, np); memcpy(h_up,
h_axp, np * sizeof(float)); memcpy(h_vp,
h_ayp, np * sizeof(float)); memcpy(h_wp,
h_azp, np * sizeof(float)); cout
<< n << endl; } free(h_xp); free(h_yp); free(h_zp); free(h_up); free(h_vp); free(h_wp); free(h_dp); free(h_xpp); free(h_ypp); free(h_zpp); free(h_axp); free(h_ayp); free(h_azp); free(h_axsp); free(h_aysp); free(h_azsp); cout
<< "end" << endl; return
0; } |