簡単なラプラス方程式を解いてみよう。2次元ラプラス方程式は
![]()
である。拡散方程式と似ているように見えるが、時間項がない。そのため、ポアソン方程式やラプラス方程式を解くときはガウス=ザイデル法やSOR法などの反復法を使って解を求める。値が収束するまで反復する。実際、差分してみると、
![]()
となり、最終的な形としては、
![]()
![]()
となる。全て、同じ時間の変数になり、拡散方程式のように単純に計算ができないため、反復して値を求める。
計算条件
IMAX 50
JMAX 50
dx 0.1
dy 0.1
初期条件
全てu=0
境界条件
j=0, 20<x<30のとき
u=10
他の境界は全て0
コードの中で注意すべき点
計算の中で、参照される値と更新される値が同じ変数のため、openmpを用いた並列計算を行うときは、工夫が必要である。
openmpの説明をすると、CPUの中には幾つのコーアが入っている。並列計算をしないと、コーア1つがfor文に従って計算を行う。例えば、
for (int j = 0; j < JMAX + 1; j++) {
for
(int i = 0; i < IMAX + 1; i++) {
x[j][i]
= dx * (double)i;
y[j][i]
= dy * (double)j;
}
}
であると、j=0, i=0でのx[0][0] = dx *
(double)0;の計算を行って、y[0][0] = dy * (double)0;の計算をする。その後 j=0, i=1となり、x[0][1] = dx *
(double)1;の計算を行って、y[0][1] = dy * (double)0;の計算を行いfor文が終わるまで繰り返す。
openmpを使ってコーア2つを使って以下のコートを並列計算を行うと、
int j,i;
#pragma omp parallel for private(i)
for (j = 0; j < JMAX + 1; j++) {
for
(i = 0; i < IMAX + 1; i++) {
x[j][i]
= dx * (double)i;
y[j][i]
= dy * (double)j;
}
}
i=0のとき、コーア1ではj=0の計算、コーア2ではj=1の計算を同時に行い、終わったら、i=1のとき、コーア1ではj=0の計算、コーア2ではj=1の計算に移る。そのため、並列計算をすると計算が早くなる。
しかい、
![]()
ような式を並列計算コードで表すと、
int i, j;
#pragma omp parallel for private(i)
for (j = 1; j < JMAX; j++) {
for
(i = 1; i < IMAX; i++) {
u1[j][i]
= ((u1[j][i - 1] + u1[j][i + 1]) / (dx*dx) + (u1[j - 1][i] + u1[j + 1][i]) /
(dy*dy))/(2.0*(1.0/(dx*dx)+1.0/(dy*dy)));
}
}
となる。よく見てみると、u1を更新するのにu1の値を使っていることがわかる。このままだと、
i=1のとき、コーア1ではj=1の計算、コーア2ではj=2の計算になり、更新される値がコーア1ではu1[1][1]、コーア2ではu1[2][1]になることがわかる。ところで、参照する部分を見ると、 u1[j - 1][i]とu1[j + 1][i]の変数があり、コーア1ではu1[2][1]、コーア2ではu1[1][1]になる部分が見られる。つまり、コーア1とコーア2で同じ変数を同時に使うことになり、CPUとしては混乱していまいため、計算がおかしくなる。このような問題を回避するために、以下のように修正する必要がある。
int i, j;
#pragma omp parallel for private(i)
for (j = 1; j < JMAX; j+=2) {
for
(i = 1; i < IMAX; i ++) {
u1[j][i]
= ((u1[j][i - 1] + u1[j][i + 1]) / (dx*dx) + (u1[j - 1][i] + u1[j + 1][i]) /
(dy*dy)) / (2.0*(1.0 / (dx*dx) + 1.0 / (dy*dy)));
}
}
#pragma omp parallel for private(i)
for (j = 2; j < JMAX; j+=2) {
for
(i = 1; i < IMAX; i ++) {
u1[j][i]
= ((u1[j][i - 1] + u1[j][i + 1]) / (dx*dx) + (u1[j - 1][i] + u1[j + 1][i]) /
(dy*dy)) / (2.0*(1.0 / (dx*dx) + 1.0 / (dy*dy)));
}
}
このように書いてあげると、コーア1ではj=1, i=1,2,3,4,5…を、コーア2ではj=3, i=1,2,3,4,5…の順番で計算をするので、変数が重複しないことがわかる。後、下のfor文ではコーア1ではj=2, i=1,2,3,4,5…を、コーア2ではj=4, i=1,2,3,4,5…の順番で計算し、最終的には全格子点に対して計算ができていることがわかる。また、上の計算方はガウス=ザイデル法であり、下のような計算方になると、SOR法である。
double u00 = 0.0, SGM=1.1;
int i, j;
#pragma omp parallel for private(i,u00)
firstprivate(SGM)
for (j = 1; j < JMAX; j += 2) {
for
(i = 1; i < IMAX; i ++) {
u00
= u1[j][i];
u1[j][i]
= ((u1[j][i - 1] + u1[j][i + 1]) / (dx*dx) + (u1[j - 1][i] + u1[j + 1][i]) /
(dy*dy)) / (2.0*(1.0 / (dx*dx) + 1.0 / (dy*dy)));
u1[j][i]
= u00 + SGM * (u1[j][i] - u00);
}
}
#pragma omp parallel for private(i,u00)
firstprivate(SGM)
for (j = 2; j < JMAX; j += 2) {
for
(i = 1; i < IMAX; i ++) {
u00
= u1[j][i];
u1[j][i]
= ((u1[j][i - 1] + u1[j][i + 1]) / (dx*dx) + (u1[j - 1][i] + u1[j + 1][i]) /
(dy*dy)) / (2.0*(1.0 / (dx*dx) + 1.0 / (dy*dy)));
u1[j][i]
= u00 + SGM * (u1[j][i] - u00);
}
}
SGMの値を1.0にすると、ガウス=ザイデル法になることがわかる。SGMの値を大きくすると、この計算を反復する回数がガウス=ザイデル法より少なくなるが、大きくし過ぎると、計算は発散する。そのため、適当な値を自ら探す必要がある。また、反復回数も値が正解に収束するまで計算する必要がある。この反復回数は格子点数に依存するため、この値も自ら探す必要がある。十分反復されているかを確認するために、変動が激しいと予想される格子点を注目し、その点での値を観察することで、反復回数を決める。
例えば、上の計算コードがcalculation_1にまとまっているとしるとmain関数の部分は以下のようになる。check0とcheck1は事前に変数を救っておいた。
for (loop = 1; loop < 2001; loop++) {
calculation_1(u1);
}
check0 = u1[2][25];
calculation_1(u1);
check1 = u1[2][25];
cout << fabs(check1 - check0) << endl;
boundary_condition(u1);
境界条件を与えるときは必ず反復が終わったあとにする。これで、fabs(check1 - check0)の結果が10-7に収まったら、値が収束できたといえるが、10-5になっても正しく計算される場合もあるため、自分の計算条件による。
Cコードは以下
#include <iostream>
#include <fstream>
#include <cmath>
#include <time.h>
#include <cstdlib>
#include <cstring>
#include <stdio.h>
#include <omp.h>
using namespace std;
#define IMAX 50
#define JMAX 50
#define dx 0.1
#define dy 0.1
int loop = 0;
void initialization_values(double u0[][IMAX + 1],
double u1[][IMAX + 1], double x[][IMAX + 1], double y[][IMAX + 1]) {
for
(int j = 0; j < JMAX + 1; j++) {
for
(int i = 0; i < IMAX + 1; i++) {
u0[j][i]
= 0.0;
u1[j][i]
= 0.0;
x[j][i]
= 0.0;
y[j][i]
= 0.0;
}
}
}
void domain(double x[][IMAX + 1], double y[][IMAX +
1]) {
for
(int j = 0; j < JMAX + 1; j++) {
for
(int i = 0; i < IMAX + 1; i++) {
x[j][i]
= dx * (double)i;
y[j][i]
= dy * (double)j;
}
}
}
void initial_condition(double u1[][IMAX + 1]) {
for
(int j = 0; j < JMAX + 1; j++) {
for
(int i = 0; i < IMAX + 1; i++) {
u1[j][i]
= 0.0;
}
}
}
void boundary_condition(double u1[][IMAX + 1]) {
for
(int i = 0; i < IMAX + 1; i++) {
u1[0][i]
= 0.0;
u1[JMAX][i]
= 0.0;
}
for
(int j = 0; j < JMAX + 1; j++) {
u1[j][0]
= 0.0;
u1[j][IMAX]
= 0.0;
}
for
(int i = 21; i < 30; i++) {
u1[0][i]
= 10.0;
}
}
void calculation_1(double u1[][IMAX + 1]) {
double
u00 = 0.0, SGM = 1.1;
int
i, j;
#pragma omp parallel for private(i,u00)
firstprivate(SGM)
for
(j = 1; j < JMAX; j += 2) {
for
(i = 1; i < IMAX; i++) {
u00
= u1[j][i];
u1[j][i]
= ((u1[j][i - 1] + u1[j][i + 1]) / (dx*dx) + (u1[j - 1][i] + u1[j + 1][i]) /
(dy*dy)) / (2.0*(1.0 / (dx*dx) + 1.0 / (dy*dy)));
u1[j][i]
= u00 + SGM * (u1[j][i] - u00);
}
}
#pragma omp parallel for private(i,u00)
firstprivate(SGM)
for
(j = 2; j < JMAX; j += 2) {
for
(i = 1; i < IMAX; i++) {
u00
= u1[j][i];
u1[j][i]
= ((u1[j][i - 1] + u1[j][i + 1]) / (dx*dx) + (u1[j - 1][i] + u1[j + 1][i]) /
(dy*dy)) / (2.0*(1.0 / (dx*dx) + 1.0 / (dy*dy)));
u1[j][i]
= u00 + SGM * (u1[j][i] - u00);
}
}
}
void write_data_vt(double u1[][IMAX + 1], double
x[][IMAX + 1], double y[][IMAX + 1]) {
ofstream
rdi;
rdi.precision(18);
char
str[20];
sprintf_s(str,
"data%d.dat", loop);// Convert i to a char
string
datafile = "./data/";
datafile.append(str);
rdi.open(datafile.c_str());
for
(int j = 0; j < JMAX + 1; j++) {
for
(int i = 0; i < IMAX + 1; i++) {
rdi
<< x[j][i] << ' ' << y[j][i] << ' ' << u1[j][i]
<< endl;
}
rdi
<< endl;
}
rdi.close();
}
int main() {
cout.precision(15);
double
check0 = 0.0, check1 = 0.0;
typedef
double IJ[IMAX + 1];
IJ
*u0, *u1, *x, *y;
u0
= (IJ *)malloc((IMAX + 1) * (JMAX + 1) * sizeof(double));
u1
= (IJ *)malloc((IMAX + 1) * (JMAX + 1) * sizeof(double));
x
= (IJ *)malloc((IMAX + 1) * (JMAX + 1) * sizeof(double));
y
= (IJ *)malloc((IMAX + 1) * (JMAX + 1) * sizeof(double));
initialization_values(u0,
u1, x, y);
domain(x,
y);
initial_condition(u1);
boundary_condition(u1);
write_data_vt(u1,
x, y);
for
(loop = 1; loop < 2001; loop++) {
calculation_1(u1);
if
(loop % 200 == 0) {
write_data_vt(u1,
x, y);
}
}
check0
= u1[2][25];
calculation_1(u1);
check1
= u1[2][25];
cout
<< fabs(check1 - check0) << endl;
boundary_condition(u1);
free(u0);
free(u1);
free(x);
free(y);
return
0;
}
Gnuplotコードは以下
reset
set terminal png #font "Times New Roman,25"
set ylabel "{/Times:Italic y}" rotate by 90
offset 0,0
set xlabel "{/Times:Italic x}" offset 0,0
set yrange[0.0:5.0]
set xrange[0.0:5.0]
set ytics offset 0,0 border 0.0,1.0,5.0
set xtics offset 0,0 border 0.0,1.0,5.0
set size ratio 1.0
set palette rgbformulae 22,13,-31
set cbtics border 0.0,0.1,1.0
set cbrange[0.0:1.0]
set view map
do for [ii=0:2000:200] {
set label 1 at graph 0.45,1.1 sprintf('n=%01.0f',ii)
set output sprintf('./png/pdata%01.0f.png',ii)
splot sprintf('./data/data%01.0f.dat',ii) with pm3d
notitle
}
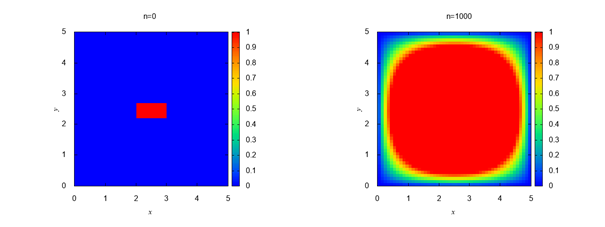
結果
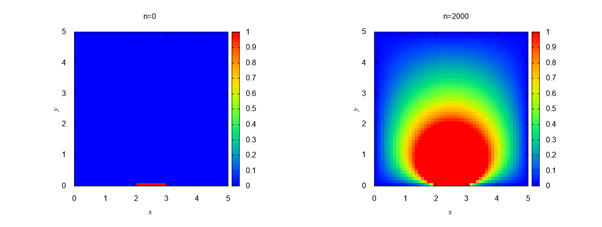
少し難易度を上げて、他の条件の計算をやってみよう。計算領域の真ん中に物体がある場合を想定する。
計算条件
IMAX 50
JMAX 50
dx 0.1
dy 0.1
初期条件
全てu=0
境界条件
22<J<27, 20<x<30のとき
u=10
他の境界は全て0
つまり、22<J<27, 20<x<30に物体があり、物体の周りの値はu=10である。物体の中は計算しない。また、計算領域に境界ができているため、それを除いて計算する必要がある。幾つか方法がある。
for文だけを利用し計算領域だけを計算する。Openmpを使っていないときを想定(コーア1つだけを利用)。
for (j = 1; j < 23; j++) {
for
(i = 1; i < IMAX; i ++) {
計算
}
}
for (j = 27; j < JMAX; j++) {
for
(i = 1; i < IMAX; i ++) {
計算
}
}
for (j = 23; j < 27; j++) {
for
(i = 1; i < 20; i ++) {
計算
}
}
for (j = 23; j < 27; j++) {
for
(i = 31; i < IMAX; i ++) {
計算
}
}
if分を使うとき
for (j = 1; j < JMAX; j++) {
if(j>22
&& j<27){
何もしない
}else{
for
(i = 1; i < IMAX; i ++) {
if(i>20
&& i<30){
何もしない
}else{
計算
}
}
}
}
または、
for (j = 1; j < JMAX; j++) {
for
(i = 1; i < IMAX; i ++) {
if(j>22
&& j<27 && i>20 && i<30){
何もしない
}else{
計算
}
}
}
基本的にif分を使うと、cpuの負担が大きくなり、計算が遅くなる。
上と下のコードを比較すると上のほうが計算負担が少ない。何故かは各自考えてみること。
計算結果をすぐ境界条件に引き返す方法
for (j = 1; j < JMAX; j++) {
for
(i = 1; i < IMAX; i ++) {
普通に計算
壁に対する境界条件だけをいれる(注意!!ノイマン条件を使うとloop前の値を入れないといけない)
}
}
ノイマン条件は後で勉強するので、今は注意が必要ということを覚えるだけでいい。上のようにすると計算された瞬間元通りになるため、for文とif分を利用した計算と同じ結果になる。
Cコード
#include <iostream>
#include <fstream>
#include <cmath>
#include <time.h>
#include <cstdlib>
#include <cstring>
#include <stdio.h>
#include <omp.h>
using namespace std;
#define IMAX 50
#define JMAX 50
#define dx 0.1
#define dy 0.1
int loop = 0;
void initialization_values(double u0[][IMAX + 1],
double u1[][IMAX + 1], double x[][IMAX + 1], double y[][IMAX + 1]) {
for
(int j = 0; j < JMAX + 1; j++) {
for
(int i = 0; i < IMAX + 1; i++) {
u0[j][i]
= 0.0;
u1[j][i]
= 0.0;
x[j][i]
= 0.0;
y[j][i]
= 0.0;
}
}
}
void domain(double x[][IMAX + 1], double y[][IMAX +
1]) {
for
(int j = 0; j < JMAX + 1; j++) {
for
(int i = 0; i < IMAX + 1; i++) {
x[j][i]
= dx * (double)i;
y[j][i]
= dy * (double)j;
}
}
}
void initial_condition(double u1[][IMAX + 1]) {
for
(int j = 0; j < JMAX + 1; j++) {
for
(int i = 0; i < IMAX + 1; i++) {
u1[j][i]
= 0.0;
}
}
}
void boundary_condition(double u1[][IMAX + 1]) {
for
(int i = 0; i < IMAX + 1; i++) {
u1[0][i]
= 0.0;
u1[JMAX][i]
= 0.0;
}
for
(int j = 0; j < JMAX + 1; j++) {
u1[j][0]
= 0.0;
u1[j][IMAX]
= 0.0;
}
for
(int j = 23; j < 27; j++) {
for
(int i = 21; i < 30; i++) {
u1[j][i]
= 10.0;
}
}
}
void calculation_1(double u1[][IMAX + 1]) {
double
u00 = 0.0, SGM = 1.1;
int
i, j;
#pragma omp parallel for private(i,u00)
firstprivate(SGM)
for
(j = 1; j < JMAX; j += 2) {
for
(i = 1; i < IMAX; i++) {
u00
= u1[j][i];
u1[j][i]
= ((u1[j][i - 1] + u1[j][i + 1]) / (dx*dx) + (u1[j - 1][i] + u1[j + 1][i]) /
(dy*dy)) / (2.0*(1.0 / (dx*dx) + 1.0 / (dy*dy)));
u1[j][i]
= u00 + SGM * (u1[j][i] - u00);
for
(int j = 23; j < 27; j++) {
for
(int i = 21; i < 30; i++) {
u1[j][i]
= 10.0;
}
}
}
}
#pragma omp parallel for private(i,u00)
firstprivate(SGM)
for
(j = 2; j < JMAX; j += 2) {
for
(i = 1; i < IMAX; i++) {
u00
= u1[j][i];
u1[j][i]
= ((u1[j][i - 1] + u1[j][i + 1]) / (dx*dx) + (u1[j - 1][i] + u1[j + 1][i]) /
(dy*dy)) / (2.0*(1.0 / (dx*dx) + 1.0 / (dy*dy)));
u1[j][i]
= u00 + SGM * (u1[j][i] - u00);
for
(int j = 23; j < 27; j++) {
for
(int i = 21; i < 30; i++) {
u1[j][i]
= 10.0;
}
}
}
}
}
void write_data_vt(double u1[][IMAX + 1], double
x[][IMAX + 1], double y[][IMAX + 1]) {
ofstream
rdi;
rdi.precision(18);
char
str[20];
sprintf_s(str,
"data%d.dat", loop);// Convert i to a char
string
datafile = "./data/";
datafile.append(str);
rdi.open(datafile.c_str());
for
(int j = 0; j < JMAX + 1; j++) {
for
(int i = 0; i < IMAX + 1; i++) {
rdi
<< x[j][i] << ' ' << y[j][i] << ' ' << u1[j][i]
<< endl;
}
rdi
<< endl;
}
rdi.close();
}
int main() {
cout.precision(15);
double
check0 = 0.0, check1 = 0.0;
typedef
double IJ[IMAX + 1];
IJ
*u0, *u1, *x, *y;
u0
= (IJ *)malloc((IMAX + 1) * (JMAX + 1) * sizeof(double));
u1
= (IJ *)malloc((IMAX + 1) * (JMAX + 1) * sizeof(double));
x
= (IJ *)malloc((IMAX + 1) * (JMAX + 1) * sizeof(double));
y
= (IJ *)malloc((IMAX + 1) * (JMAX + 1) * sizeof(double));
initialization_values(u0,
u1, x, y);
domain(x,
y);
initial_condition(u1);
boundary_condition(u1);
write_data_vt(u1,
x, y);
for
(loop = 1; loop < 1001; loop++) {
calculation_1(u1);
if
(loop % 50 == 0) {
write_data_vt(u1,
x, y);
}
}
check0
= u1[28][25];
calculation_1(u1);
check1
= u1[28][25];
cout
<< fabs(check1 - check0) << endl;
boundary_condition(u1);
free(u0);
free(u1);
free(x);
free(y);
return
0;
}
Gnuplotコード
reset
set terminal png #font "Times New Roman,25"
set ylabel "{/Times:Italic y}" rotate by 90
offset 0,0
set xlabel "{/Times:Italic x}" offset 0,0
set yrange[0.0:5.0]
set xrange[0.0:5.0]
set ytics offset 0,0 border 0.0,1.0,5.0
set xtics offset 0,0 border 0.0,1.0,5.0
set size ratio 1.0
set palette rgbformulae 22,13,-31
set cbtics border 0.0,0.1,1.0
set cbrange[0.0:1.0]
set view map
do for [ii=0:1000:50] {
set label 1 at graph 0.45,1.1 sprintf('n=%01.0f',ii)
set output sprintf('./png/pdata%01.0f.png',ii)
splot sprintf('./data/data%01.0f.dat',ii) with pm3d
notitle
}
結果