ó¬ÝÂÐÎÞÄ

変数 u ª¬ÍöÊàñ¨øö x,y ªËëîðíª¹ªëªÈª¤ª¦2ó­êªÙýð¹ªòÍŪ¨ªë¡£

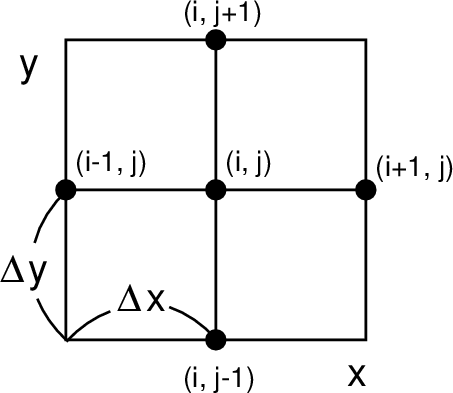
_images/mesh.png

2ó­êª«á«Ã«·«åªÎ図

2ó­êªÍöÊàªò図ªÎªèª¦ªÊÌ«í­ªË区﷪ꡢÊÀÌ«í­ïêÎñ¨øöªò (x_i, y_j) ªÈª¹ªë¡£Ì«í­ÊàÌ°ªÏ x Û°ú¾ª¬ \Delta x ¡¢ y Û°ú¾ª¬ \Delta y ªÈª¹ªë¡£ x_{i \pm 1} = x_i \pm \Delta x ¡¢ y_{j \pm 1} = y_j \pm \Delta y ªÇª¢ªë¡£ì¤ù»¡¢Ì«í­ïÃÛã号 (i,j) ªòéĪ¤ªÆ u_{i,j} = u(x_i, y_j) ªÎªèª¦ªËÕÔÑÀª¹ªë¡£

ó·Ùͪ·ªÆª¤ªëïà(x_i, y_j) ªÎªÞªïªêªÇ«Æ«¤«éーî÷ËÒª¹ªëªÈ¡¢

(1)u_{i+1,j} = u(x_i+\Delta x, y_j) = u_{i,j} +\Delta x \left (\displaystyle{{\partial u} \over {\partial x}} \right)_i +\displaystyle{{{\Delta x}^2} \over {2!}} \left (\displaystyle{{\partial^2 u} \over {\partial x^2}} \right)_i +\displaystyle{{{\Delta x}^3} \over {3!}} \left (\displaystyle{{\partial^3 u} \over {\partial x^3}} \right)_i + ...

(2)u_{i-1,j} = u(x_i-\Delta x, y_j) = u_{i,j} -\Delta x \left (\displaystyle{{\partial u} \over {\partial x}} \right)_i +\displaystyle{{{\Delta x}^2} \over {2!}} \left (\displaystyle{{\partial^2 u} \over {\partial x^2}} \right)_i -\displaystyle{{{\Delta x}^3} \over {3!}} \left (\displaystyle{{\partial^3 u} \over {\partial x^3}} \right)_i + ...

ãÒ (1) ª«ªéãÒ (2) ªòìÚª¯ªÈ

(3)u_{i+1,j} - u_{i-1,j} = 2\Delta x \left (\displaystyle{{\partial u} \over {\partial x}}\right )_i + O(\Delta x^3)

ª·ª¿ª¬ªÃªÆ¡¢

(4)\left (\displaystyle{{\partial u} \over {\partial x}} \right )_i = \displaystyle{{u_{i+1,j} - u_{i-1,j}} \over {2\Delta x}} + O(\Delta x^2)

ª¹ªÊªïªÁ¡¢ (i,j) ïê˪ªª±ªë u ªÎ x Û°ú¾ªÎÚ°ÝÂÌõ数 (\partial u/\partial x)_i ª¬ \Delta x^2 ªÎè¦ó¬ªòùߪàÐÎÞĪΪâªÈªÇ( \Delta x ªËªÄª¤ªÆ2ó­ªÎïñÓøªÇ)ì¤ù»ªÎªèª¦ªËÏ´ªÞªë¡£

(5)\left (\displaystyle{{\partial u} \over {\partial x}} \right)_i = \displaystyle{{u_{i+1,j} - u_{i-1,j}} \over {2\Delta x}}

ª³ªìªòñéãýó¬ÝªÎãÒªÈå몦¡£

ÔÒ様ªËª·ªÆ¡¢ \Delta x ªËªÄª¤ªÆ1ó­ªÎïñÓøªÇì¤ù»ªÎó¬ÝÂÐÎÞÄãÒª¬Ôðªéªìªë¡£

îñòäó¬Ý£º

(6)\left (\displaystyle{{\partial u} \over {\partial x}}\right)_i = \displaystyle{{u_{i+1,j} - u_{i,j}} \over {\Delta x}}

ý­÷Üó¬Ý£º

(7)\left(\displaystyle{{\partial u} \over {\partial x}}\right)_i = \displaystyle{{u_{i,j} - u_{i-1,j}} \over {\Delta x}}

ãÒ (1) ªÈãÒ (2) ªòÊ¥ª¨ªëªÈ

(8)u_{i+1,j} + u_{i-1,j} = 2u_{i,j} + \Delta x^2 \left(\displaystyle{{\partial^2 u} \over {\partial x^2}}\right)_i + O(\Delta x^4)

ª·ª¿ª¬ªÃªÆ¡¢

(9)\left(\displaystyle{{\partial^2 u} \over {\partial x^2}}\right)_i = \displaystyle{{u_{i+1,j} - 2u_{i,j} + u_{i-1,j}} \over {\Delta x^2}} + O(\Delta x^2)

ª³ªìªèªê¡¢ u ªÎ x ªË関ª¹ªë2ͭڰݪÎÌõ数 (\partial^2 u/\partial x^2)_i ªò \Delta x ªËªÄª¤ªÆ2ó­ªÎïñÓøªÇì¤ù»ªÎªèª¦ªËÐÎÞĪ¹ªëª³ªÈª¬ªÇª­ªë¡£

(10)\left(\displaystyle{{\partial^2 u} \over {\partial x^2}}\right)_i = \displaystyle{{u_{i+1,j} - 2u_{i,j} + u_{i-1,j}} \over {\Delta x^2}}

ÔÒ様ªË¡¢

(11)\left(\displaystyle{{\partial^2 u} \over {\partial y^2}}\right)_j = \displaystyle{{u_{i,j+1} - 2u_{i,j} + u_{i,j-1}} \over {\Delta y^2}}.

 

\left(\displaystyle{{\partial^2 u} \over {\partial y^2}}\right)_j = \displaystyle{{u_{i,j+1} - 2u_{i,j} + u_{i,j-1}} \over {\Delta y^2}}.

àÊû¡«¹«««éーì¹×µÛ°ïïãÒªÎó¬ÝÂú°Ûö

£±ó­êªàÊû¡«¹«««éーì¹×µÛ°ïïãÒ

×µ体・í¸気×µ体Û°ïïãÒªÎÜâòõªÏ÷îªÎ伝÷ëªËª¢ªë¡£ª³ªÎݻݪÀª±ªòö¢ªêõóª·ªÆó­ªÎªèª¦ªÊÛ°ïïãÒªòÍŪ¨ªë¡£

(12)\displaystyle{{\partial u} \over {\partial t}} + c \displaystyle{{\partial u} \over {\partial x}} = 0

ª¿ªÀª·¡¢ c ªÏïÒ数ªÇ c > 0 ªÈª¹ªë¡£ª³ªÎÛ°ïïãҪϡ¢«¹«««éーÕá u ªÎÍöÊàÝÂøÖª¬¡¢ìéïÒªÎáÜÓø c ªÇ伝÷몹ªëª³ªÈªòª¢ªéªïª¹÷îÔÑÛ°ïïãҪǪ¢ªë¡£

Û°ïïãÒ (12) ªÎ厳ÚËú°ªÏ

(13)u(x,t) = u(x-ct,0)

ªÇª¢ªë¡£ª³ªìªÏ¡¢ãÁʾ t > 0 ªËªªª±ªë«¹«««éーÕá u ªÎ«×«í«Õ«£ー«ëªÏ t=0 ªÎ«¹«««éーÕá u ªÎ«×«í«Õ«£ー«ëª¬û¡ªòÜÁªÃªÆ ct ªÀª±øÁú¼ì¹ÔѪ·ª¿û¡ªËªÊªëª³ªÈªòª¢ªéªïª¹¡£

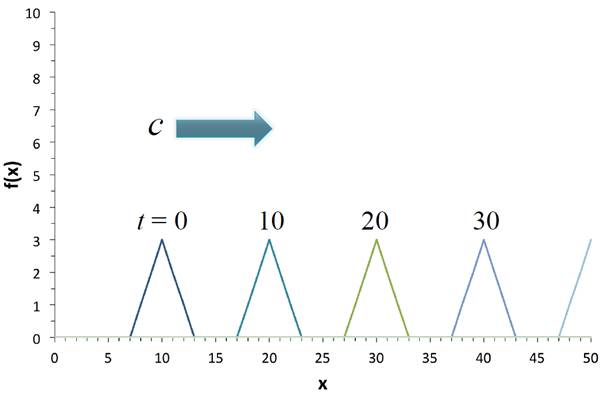
ì¹×µÛ°ïïãÒªÎ厳ÚËú°

ª¤ªÞ¡¢図 1ó­êª«¹«««éーì¹×µÙýð¹ªÎôøÑ¢条ËìªÈãÁÊà発î÷ ªÎªèª¦ªËôøÑ¢ªË x \ge 0 ªÇ u=u_1 ¡¢ x < 0 ªÇ u=u_2 ªÎªèª¦ªË x=0 ªÇÜôÖ§続ªÊÝÂøÖªòÍŪ¨ªÆªßªëªÈ t > 0 ªÇªÎ厳ÚËú°ªÏéÓ図ªÎªèª¦ªÊû¡ªËªÊªë¡£

 

参ÍÅÙþ献

http://www.astro.phys.s.chiba-u.ac.jp/cans/doc/sabun.html

 

ͪߩ条ËìªÏì¤ù»ªËªÊªë¡£

x Û°ú¾ªËÔõÊàÌ°ªË51Ì«í­(IMAX=51)ªÈª¹ªë¡£¥Äx = 1 m¡¢¥Ät = 1 s ªÈª¹ªë¡£ãÁÊàªÏ50sªÞªÇ(NMAX=50)ͪߩª¹ªë¡£c=0.3¡£

ôøÑ¢条ËìªÏ

ÌÑÍ£条ËìªÏ

f(0)=0.0, f(IMAX)=0.0ªÈª¹ªë¡£

ãÁÊàú£ªË関ª·ªÆªÏîñòäó¬Ý¡¢ì¹×µú£ªËªÄª¤ªÆªÏñéãýó¬Ýª˪¹ªëª³ªÈ¡£Source.cppª¬ìýªÃªÆª¤ªë«Õ«©«ë«ÀーªËdataªÈpngªÎ«Õ«©«ë«Àーªòíªêƪªª¯ª³ªÈ¡£

ì¤ù»ªÏ«³ー«ÉªÇª¢ªë¡£

C++«³ー«É

#include <iostream>

#include <fstream>

#include <cmath>

#include <time.h>

#include <cstdlib>

#include <cstring>

#include <stdio.h>

#include <omp.h>

using namespace std;

#define NMAX 50

#define IMAX 51

#define dx 1.0

#define dt 1.0

#define c 0.3

int n = 0;

void initialization_values(double u0[], double u1[], double x[]) {

                  for (int i = 0; i < IMAX + 1; i++) {

                                    u0[i] = 0.0;

                                    u1[i] = 0.0;

                                    x[i] = 0.0;

                  }

}

void domain(double x[]) {

                  for (int i = 0; i < IMAX + 1; i++) {

                                    x[i] = dx * (double)i;

                  }

}

void initial_condition(double u1[]) {

                  for (int i = 0; i < 7; i++) {

                                    u1[i] = 0.0;

                  }

                  for (int i = 7; i < 11; i++) {

                                    u1[i] = (double)i - 7.0;

                  }

                  for (int i = 11; i < 14; i++) {

                                    u1[i] = -(double)i + 13.0;

                  }

                  for (int i = 14; i < IMAX + 1; i++) {

                                    u1[i] = 0.0;

                  }

}

void boundary_condition(double u1[]) {

                  u1[0] = 0.0;

                  u1[IMAX] = 0.0;

}

void calculation_1(double u0[], double u1[]) {

                  int i;

#pragma omp parallel for

                  for (i = 1; i < IMAX; i++) {

                                    u1[i] = u0[i] - dt * c*(u0[i + 1] - u0[i - 1]) / (2.0*dx);

                  }

}

void write_data_vt(double u1[], double x[]) {

                  ofstream rdi;

                  rdi.precision(18);

                  char str[20];

                  sprintf_s(str, "data%d.dat", n);// Convert i to a char

                  string datafile = "./data/";

                  datafile.append(str);

                  rdi.open(datafile.c_str());

                  for (int i = 0; i < IMAX + 1; i++) {

                                    rdi << x[i] << ' ' << u1[i] << endl;

                  }

                  rdi.close();

}

int main() {

                  cout.precision(15);

                  typedef double I;

                  I *u0, *u1, *x;

                  u0 = (I *)malloc((IMAX + 1) * sizeof(double));

                  u1 = (I *)malloc((IMAX + 1) * sizeof(double));

                  x = (I *)malloc((IMAX + 1) * sizeof(double));

                  initialization_values(u0, u1, x);

                  domain(x);

                  initial_condition(u1);

                  boundary_condition(u1);

                  write_data_vt(u1, x);

                  for (n = 1; n < NMAX + 1; n++) {                              

                                    memcpy(u0, u1, (IMAX + 1) * sizeof(double));

                                    calculation_1(u0, u1);

                                    boundary_condition(u1);

                                    write_data_vt(u1, x);

                  }

                  free(u0);

                  free(u1);

                  free(x);

                  return 0;

}

GnuplotªÎ«³ー«É

reset

set terminal png font "Times New Roman,25"

set ylabel "{/Times:Italic u}" rotate by 90 offset 0,0

set xlabel "{/Times:Italic x}" offset 0,0

set yrange[-5.0:5.0]

set xrange[0:50]

set ytics offset 0,0 border -5.0,1.0,5.0

set xtics offset 0,0 border 0,5,50

do for [ii=0:50:1] {

set output sprintf('./png/pdata%01.0f.png',ii)

plot sprintf('./data/data%01.0f.dat',ii) using 1:2 with line lw 5 lc "red" title sprintf('{/Times:Italic t}=%01.0f',ii)

}

ì¤ù»ªÏÌ¿Íý

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

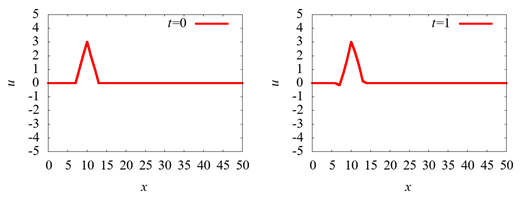
ì¹×µú£ªòñéãýó¬ÝªÇú°ª¯ªÈÜôäÌïҪ˪ʪ롣

ª½ª³ªÇ¡¢ù¦ß¾ó¬ÝÂÛöªòÞŪ¦¡£

1ó­ù¦ß¾ó¬ÝÂ

3ó­ù¦ß¾ó¬ÝÂ

ì¹×µú£ªÎͪߩªò1ó­ªÈ3ó­ïñÓøªÎù¦ß¾ó¬ÝªòéĪ¤ªÆͪߩªòª¹ªë¡£

1ó­ù¦ß¾ó¬ÝªÏÌÑÍ£Øüª«ªé1ËÁ×îªìª¿Ì«í­(ÖǪ¨ªÐi=1ªÈi=IMAX-1)ªÇÞŪ¦¡£残ªêªÎÌ«í­ªÇªÏ3ó­ïñÓøªÎù¦ß¾ó¬ÝªòÞŪ¦¡£

C++«³ー«ÉªÏì¤ù»ªËªÊªë

#include <iostream>

#include <fstream>

#include <cmath>

#include <time.h>

#include <cstdlib>

#include <cstring>

#include <stdio.h>

#include <omp.h>

using namespace std;

#define NMAX 50

#define IMAX 51

#define dx 1.0

#define dt 1.0

#define c 0.3

int n = 0;

void initialization_values(double u0[], double u1[], double x[]) {

                  for (int i = 0; i < IMAX + 1; i++) {

                                    u0[i] = 0.0;

                                    u1[i] = 0.0;

                                    x[i] = 0.0;

                  }

}

void domain(double x[]) {

                  for (int i = 0; i < IMAX + 1; i++) {

                                    x[i] = dx * (double)i;

                  }

}

void initial_condition(double u1[]) {

                  for (int i = 0; i < 7; i++) {

                                    u1[i] = 0.0;

                  }

                  for (int i = 7; i < 11; i++) {

                                    u1[i] = (double)i - 7.0;

                  }

                  for (int i = 11; i < 14; i++) {

                                    u1[i] = -(double)i + 13.0;

                  }

                  for (int i = 14; i < IMAX + 1; i++) {

                                    u1[i] = 0.0;

                  }

}

void boundary_condition(double u1[]) {

                  u1[0] = 0.0;

                  u1[IMAX] = 0.0;

}

void calculation_1(double u0[], double u1[]) {

                  int i;

#pragma omp parallel for

                  for (i = 1; i < IMAX; i += IMAX - 2) {

                                    u1[i] = u0[i] - dt * (c*(-u0[i - 1] + u0[i + 1]) / (2.0*dx) + fabs(c)*(-u0[i - 1] + 2.0*u0[i] - u0[i + 1]) / (2.0*dx));

                  }

#pragma omp parallel for

                  for (i = 2; i < IMAX - 1; i ++) {

                                    u1[i] = u0[i] - dt * (c*(u0[i - 2] + 8.0*(-u0[i - 1] + u0[i + 1]) - u0[i + 2]) / (12.0*dx) + fabs(c)*(u0[i - 2] - 4.0*u0[i - 1] + 6.0*u0[i] - 4.0*u0[i + 1] + u0[i + 2]) / (12.0*dx));

                  }

}

void write_data_vt(double u1[], double x[]) {

                  ofstream rdi;

                  rdi.precision(18);

                  char str[20];

                  sprintf_s(str, "data%d.dat", n);// Convert i to a char

                  string datafile = "./data/";

                  datafile.append(str);

                  rdi.open(datafile.c_str());

                  for (int i = 0; i < IMAX + 1; i++) {

                                    rdi << x[i] << ' ' << u1[i] << endl;

                  }

                  rdi.close();

}

int main() {

                  cout.precision(15);

                  typedef double I;

                  I *u0, *u1, *x;

                  u0 = (I *)malloc((IMAX + 1) * sizeof(double));

                  u1 = (I *)malloc((IMAX + 1) * sizeof(double));

                  x = (I *)malloc((IMAX + 1) * sizeof(double));

                  initialization_values(u0, u1, x);

                  domain(x);

                  initial_condition(u1);

                  boundary_condition(u1);

                  write_data_vt(u1, x);

                  for (n = 1; n < NMAX + 1; n++) {

                                    memcpy(u0, u1, (IMAX + 1) * sizeof(double));

                                    calculation_1(u0, u1);

                                    boundary_condition(u1);

                                    write_data_vt(u1, x);

                  }

                  free(u0);

                  free(u1);

                  free(x);

                  return 0;

}

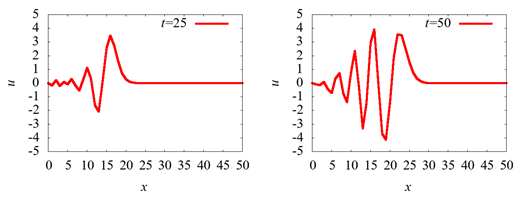
Ì¿ÍýªÏù»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

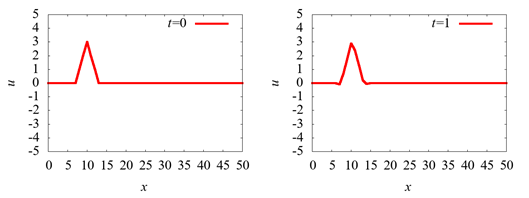
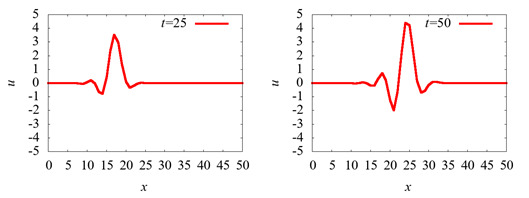
ñéãýó¬ÝªèªêªÏªÞª·ªËªÊªÃª¿¡£

 

c=1.0ªÎͪߩ̿Íý

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

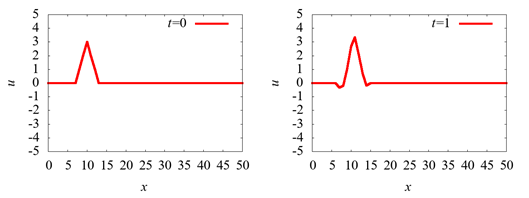
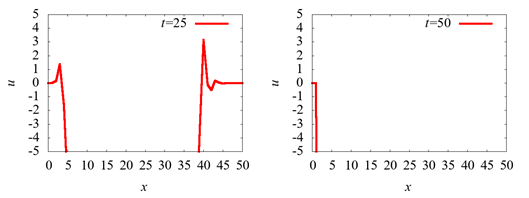
ͪߩª¬÷ò÷ªª·ªÞª¦¡£

CFL条Ëìªòü¬ìã¡£

ªò満ª¿ªµªÊª¤ªÈͪߩªÏ÷ò÷ªª·ªÞª¦¡£×µ体ªÎͪߩªÇªÏ

ªò満ª¿ª·ª¿ªÛª¦ª¬äÌîï¡£仮ªËͪߩªÇª­ªÆªâª½ªÎÌ¿Íýª¬ï᪷ª¤ªÈªÏå모ªÊª¤¡£