2. LibreOffice　におけるマクロのコード実行例¶

2.1. 例題１¶

100℃、1 atmにおける水の蒸発熱は9720 cal/molである。27℃,1 atmにおける水の蒸発熱を求めなさい。ただし、水のモル熱容量は18.06 cal/Kmolと一定であり、水蒸気のモル熱容量は以下の式で近似される。

\[C_p=7.219 + 2.374 \times \rm{10}^{-3} T + 2.67 \times \rm{10}^{-7} T^2\]

蒸発反応は以下の化学式である。

\[\rm{H_2O(l) →H_2O(g)}\]

2.2. 例題1の回答¶

考え方として、

\[\Delta H_{27} = \Delta H_{100} - \int_{27}^{100} \Delta C_p dT\]

\[\Delta C_p = 7.219-18.06 + 2.374 \times \rm{10}^{-3} T + 2.67 \times \rm{10}^{-7} T^2\]

の２つの式を使う。

必要な値を LibreOffice calc のセルに打ち込み、計算すると以下のようになる。

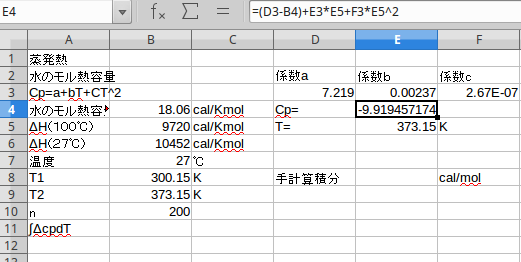
積分によって, \(\int\Delta C_p dT\) を求めたい。勿論、手計算によって積分することが出来る。その場合、 E8セル に入力する式は

\[\int_{27}^{100} \Delta C_p dT = (D3-B4)*(B9-B8) + E3/2*(B9^2-B8^2)+F3/3*(B9^3-B8^3)\]

となる。結果は以下の図である。

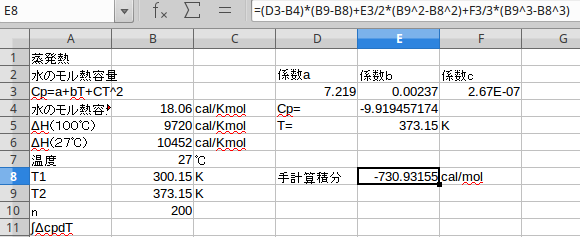
一応の回答は -730.9 {cal/mol} と算出出来た。よって、

\[\Delta H_{27} = 9720 - (-730.9)\]

\(\Delta H_{27}\) = 10450.9 {cal/mol} と計算できた。しかし、この書き方では入力式が長くなりミスも生じやすい。マクロを記述し、それを利用する。

2.3. マクロのコード¶

Sub simpson()

サブルーチンの始まりを定義。　名前は simpson

Dim doc As Object
Dim sheet As Object
Dim cell As Object
Dim oNumberFormats As Object

「Dim」文 は変数の宣言。 doc という名前の変数をオブジェクト型として宣言する。

doc=ThisComponent
'Sheet=doc.sheets(2)
sheet=doc.CurrentSelection.spreadsheet

doc を現在アクティブなドキュメントとして指定。この場合は保存したシート。

t1=sheet.getCellByPosition(1,7).Value
t2=sheet.getCellByPosition(1,8).Value
n=sheet.getCellByPosition(1,9).Value
h=(t2-t1)/n
sheet.getCellByPosition(4,4).Value=t1
ft1=sheet.getCellByPosition(4,3).Value
sheet.getCellByPosition(4,4).Value=t2
ft2=sheet.getCellByPosition(4,3).Value
fsum=ft1+ft2

積分値の上限と下限として、 t1 , t2 を設定。それぞれ対応するセルの値を代入。 ｎ は試行回数、 ft1 , ft2 はCpの式にしたがって計算し、条件温度を当てはめて値を設定する。

fsum で合計する。 ft1 と ft2 の処理を合計する。

for i=1 to n-1 step 2
 sheet.getCellByPosition(4,4).Value=t1+h*i
 fi=sheet.getCellByPosition(4,3).Value
 sheet.getCellByPosition(4,4).Value=t1+h*(i+1)
 fj=sheet.getCellByPosition(4,3).Value
 fsum=fsum+4*fj+2*fi

next i 

for文 のループを構築する。ここの処理で200回の積分の試行のループを回す。

sheet.getCellByPosition(1,10).Value=h/3*fsum

End Sub

#セルB11に結果を出力する。

#サブルーチンの終わり

このマクロを用いて計算すれば、結果は下の図になる。

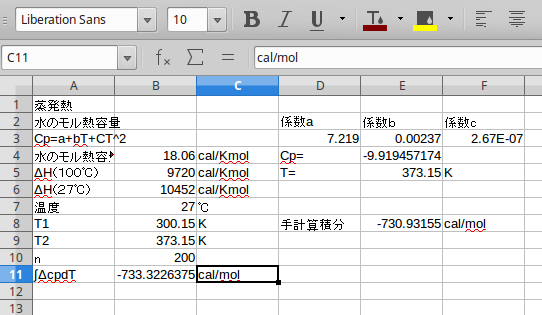
-733.3 cal/molを得ることが出来た。

\[\Delta H_{27} = 9720 - (-733.3)\]

よって、　\(\Delta H_{27}\) = 10450.9{cal/mol} を得た。

2.4. 例題２¶


T(K)	10	20	30	40	50	60	70	80	90
Cp(J/Kmol)	2.09	14.43	36.44	62.55	87.03	111	131.4	149.4	165.3
T(K)	100	110	150	160	170	180	190	200
Cp(J/Kmol)	179.6	192.8	237.6	247.3	256.5	265.1	273	280.3

無水ヘキサシアノ鉄（2）酸カリウムの熱容量は上の表のように変化する。

表の各温度で、 \(T=0\) を基準にしたモルエンタルピー \({H_m}(T) - H_m (0)\) と第三法則エントロピー \(S_T\) を計算せよ。

2.5. 例題２の回答¶

\[ \begin{align}\begin{aligned}S_{T1} = \int_{0}^{T1} \displaystyle \frac{ C_p }{ T } dT\\H_m(T) - H_m(0) = \int_{0}^{T} C_p dT\end{aligned}\end{align} \]

横軸 \(T\) 、縦軸 \(C_p\) ないしは \(C_p /T\) のプロットを行い、グラフの面積を求めれば良い。

まず必要な値を LibreOffice calc のセルに打ち込み、横軸を T 、縦軸を \(C_p\) でプロットし、 4次の多項式で近似させ、近似値の係数を取り出すと次のようになる。

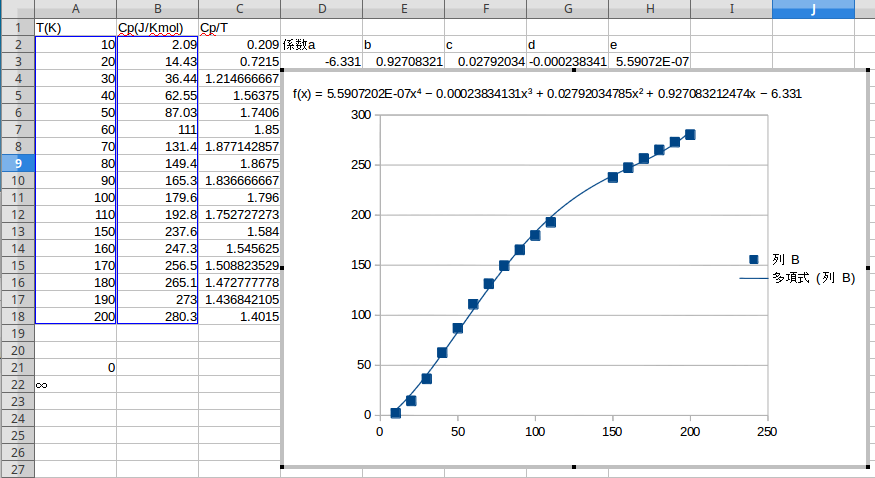
よって、\(C_p\) は下の式になる。

\[C_p = -6.331 + 9.271 \times \rm{10}^{-1} T + 2.792 \times \rm{10}^{-2} T^2 - 2.383 \times \rm{10}^{-4} T^3 + 5.591 \times \rm{10}^{-7} T^4\]

これを、後述するマクロによって積分し、\({H_m}(T) - H_m(0)\) の値を B20 に出力すると、以下の図のようになる。

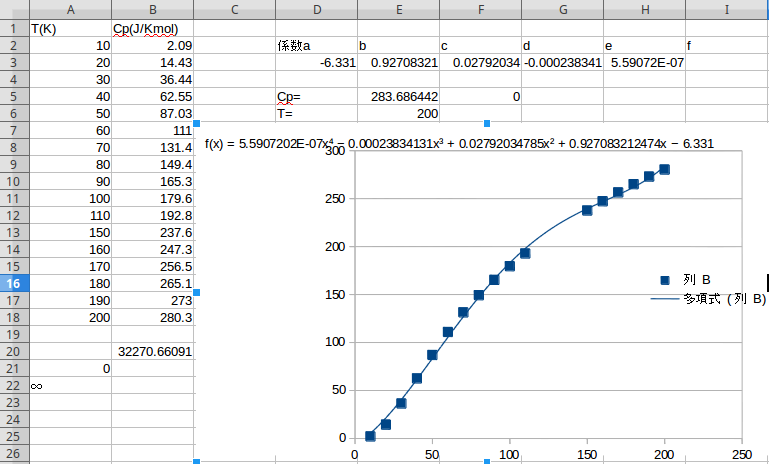
よって、\({H_m} (T) - H_m(0)\) は 32.27 kJ となった

また、 \(S_T\) についても同様に横軸を \(T\) 、縦軸を \(C_p\)/Tでプロットし、4次の多項式で近似させ近似値の係数を取り出せば次のようになる。

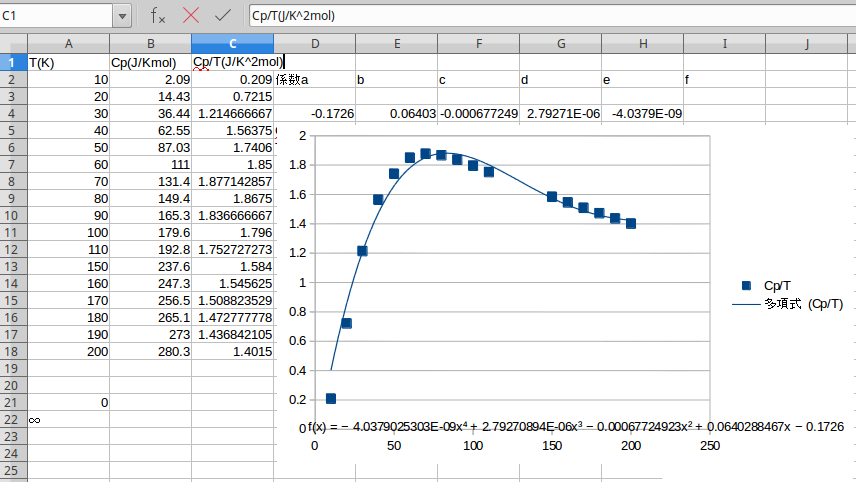
よって、\(C_p/T\) は下の式になる。

\[C_p/T = -0.1726 + 6.403 \times \mathrm{10}^{-2} T - 6.7725 \times \mathrm{10}^{-4} T^2 - 2.7927 \times \mathrm{10}^{-6} T^3 - 4.0379 \times \mathrm{10}^{-9} T^4\]

これを、後述するマクロによって積分し、 \(S_T\) の値を B21 に出力すると、以下の図のようになる。

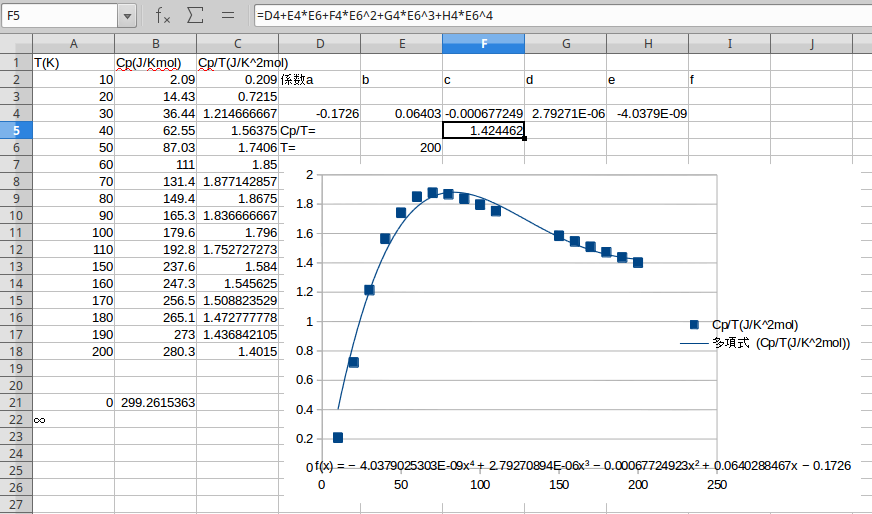
よって、 \(S_T\) は 299 J/K となった。

2.6. 例題２の \(H\) を求めるマクロのコード¶

# -*- coding: utf-8 -*-
"""
Created on Wed May 30 16:14:32 2018

@author: user
"""

sub simpson()

Dim doc As Object
Dim sheet As Object
Dim cell As Object
Dim oNumberFormats As Object

doc=ThisComponent
'sheet=doc.sheets(2)
sheet=doc.CurrentSelection.spreadsheet

t1=sheet.getCellByPosition(0,20).Value
t2=sheet.getCellByPosition(0,17).Value
n=200
h=(t2-t1)/n

sheet.getCellByPosition(4,5).Value=t1
ft1=sheet.getCellByPosition(4,4).Value
sheet.getCellByPosition(4,5).Value=t2
ft2=sheet.getCellByPosition(4,4).Value
fsum=ft1-ft2

for i=1 to n-1 step 2
 sheet.getCellByPosition(4,5).Value=t1+h*i
 fi=sheet.getCellByPosition(4,4).Value
 sheet.getCellByPosition(4,5).Value=t1+h*(i+1)
 fj=sheet.getCellByPosition(4,4).Value
 fsum=fsum+4*fj+2*fi

next i
sheet.getCellByPosition(1,19).Value=h/3*fsum


End Sub

2.7. 例題２の \(S\) を求めるマクロのコード¶

# -*- coding: utf-8 -*-
"""
Created on Wed May 30 16:10:26 2018

@author: user
"""

sub simpson()

Dim doc As Object
Dim sheet As Object
Dim cell As Object
Dim oNumberFormats As Object

doc=ThisComponent
'sheet=doc.sheets(2)
sheet=doc.CurrentSelection.spreadsheet

t1=sheet.getCellByPosition(0,20).Value
t2=sheet.getCellByPosition(0,17).Value
n=200
h=(t2-t1)/n

sheet.getCellByPosition(4,5).Value=t1
ft1=sheet.getCellByPosition(5,4).Value
sheet.getCellByPosition(4,5).Value=t2
ft2=sheet.getCellByPosition(5,4).Value
fsum=ft1-ft2

for i=1 to n-1 step 2
 sheet.getCellByPosition(4,5).Value=t1+h*i
 fi=sheet.getCellByPosition(5,4).Value
 sheet.getCellByPosition(4,5).Value=t1+h*(i+1)
 fj=sheet.getCellByPosition(5,4).Value
 fsum=fsum+4*fj+2*fi

next i
sheet.getCellByPosition(1,20).Value=h/3*fsum


End Sub

警告

マクロを記述する時の注意点

マクロはアクティブなシートのセルを参照するが、その番号が一つずつずれて認識されている。例えば A1 は、マクロで (0,0) となる。
マクロを記録した LibreOffice calc を起動する時に必ず [マクロを有効にする] を許可しなければならない。
保存場所に注意。

2. LibreOffice におけるマクロのコード実行例¶