2. 序論¶
2.1. jupyter notebook について¶
pythonは科学技術計算の分野では最近注目を浴びている言語で、プログラミング初学者が 習得しやすい言語の一つとして知られている。フリーで windows、mac、linuxなど動作する環境が幅広い。その上、数値計算に必要な信頼性の高いライブラリーがそろっており、特に深層学習や機械学習ではアルゴリズムの実装に良く使われている。 jupyter notebook (https://jupyter.org/)は、対話型python環境で、ユーザーがプログラムの断片やデータの一部を入力して、試行錯誤を行い、その結果や振る舞いを眺めながら考える環境を与えることができ、 さらにそれらを共有、追体験できるのである。また、 jupyter notebook で生成されるnotebookはネット上に公開し知識を共有するのに適している。 jupyter notebook 上での解析工程は一般的な現代データサイエンス解析のワークフローに順じており、その使い方に慣れることは 異分野間でのコミュニケーションだけでなく、学生諸君に対しても教育効果は高いと思われる。 残念ながら巷であふれている jupyter notebook の使い方の情報はcsvファイル形式の汎用データベースに関してが主で、 実験データの処理に関して言及されているものは少ない。
本稿ではタンパク質溶液散乱の解析フローを jupyter-notebook で実行することにより、タンパク質溶液散乱で良く使われるデータ形式の ファイルを jupyter-notebook で取り扱うための概要を紹介する。
2.2. 実行までの準備¶
jupyter-notebook を導入するには、 最初にpythonをインストールしてその後に jupyter-notebook を使えるようにする。この方法については インターネットを探せば、様々な情報が得られる。筆者のおすすめは最も簡単な方法は、 Anaconda と呼ばれるデータサイエンスに特化したpythonの無料ディストリビューションの一部として jupyter-notebook をインストールするのが便利である。
Anaconda は、以下のサイトから ダウンロードすることができる。
https://www.anaconda.com/download
windows、 mac、 linux 向けにインストーラーが 準備されている。 インストールする際にはpythonのバージョンを選択しないといけないが、 サポートが終了した2.7よりは3.xを選択するほうが良いであろう。
元々、 Anaconda はデータサイエンスに特化したプラットフォームを提供したいというのが目的なので、 それ用によく使われる一連のpythonパッケージ群が同梱されている。
jupyter-notebook を起動するにはターミナルを開きコマンドプロンプトで:
jupyter-notebook
と打てば、勝手にブラウザーが立ち上がる。
デフォルトでは、3次元構造の pdb フォーマットを取り扱えないので、
nglview [1] というwidgetをインストールする。
https://github.com/arose/nglview
コマンドプロンプトで:
conda install nglview -c conda-forge
jupyter-nbextension enable nglview --py --sys-prefix
でエラーがでなければ大丈夫である。グラフィックボード環境の違いにより表示されたりされなかったりすることもあるが、 このwidgetを使えば、3次元構造を jupyter-notebook 上でぐるぐる回すことができるようになる。
また、本稿ではEMBL Hamburgの小角散乱グループが開発したタンパク質溶液散乱の標準的パッケージ ATSAS を使用する [2] 。以下のサイトでユーザー登録すると無料でダウンロードできるのであらかじめインストールしておく。
2.3. 本稿で取り扱うデータ解析の流れ¶
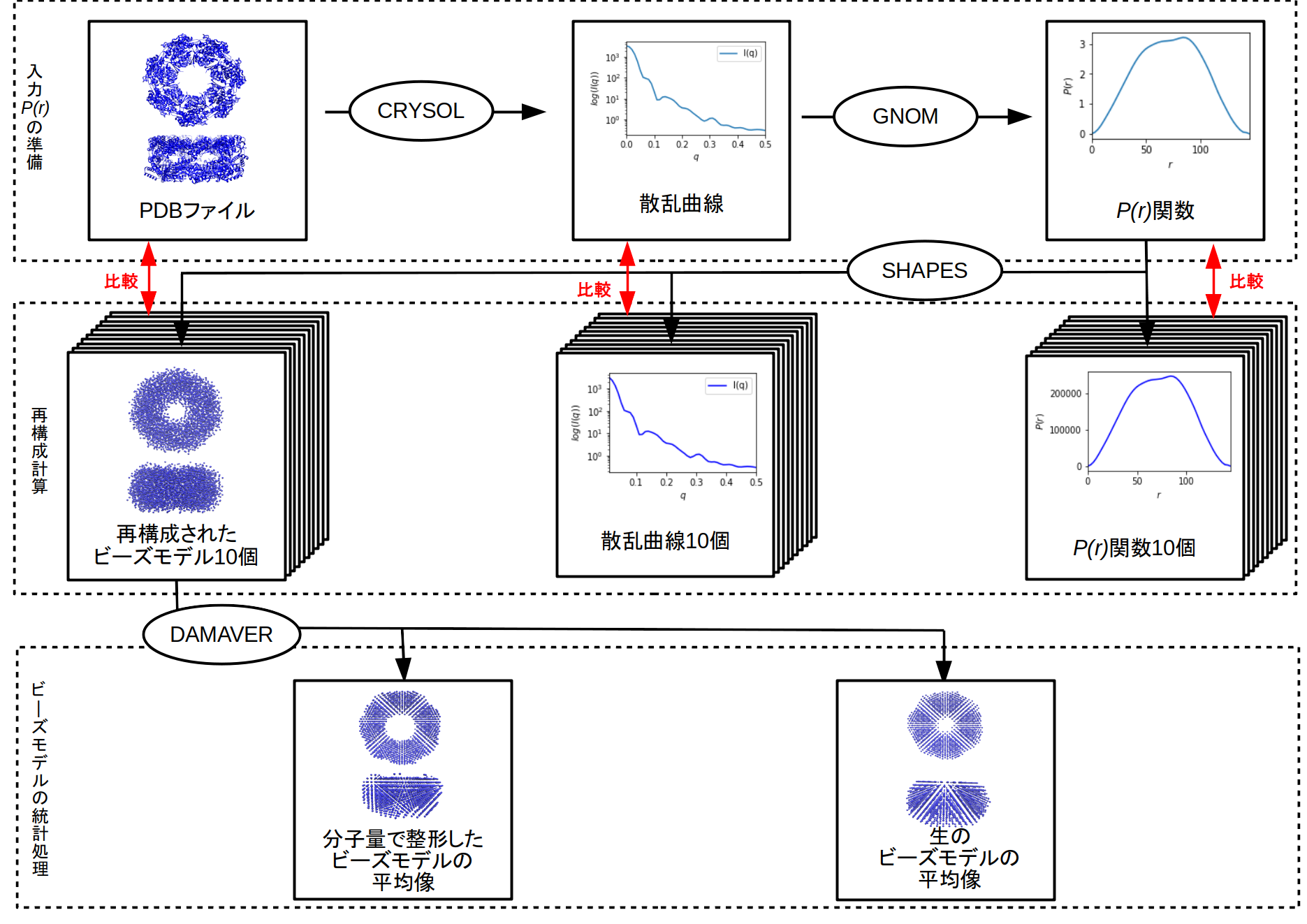
本稿では jupyter-notebook を用いてタンパク質溶液散乱データの読み方、プロットの仕方などを初心者がつまづきやすい点を中心に紹介していきたい。 タンパク質溶液散乱では、最も一般的な解析は散乱データからタンパク質構造を充填球で近似したいわゆるビーズモデルを計算することである。 ATSAS で使用される代表的なフォーマットのファイルを扱うよう、以下のデータ解析を jupyter-notebook で処理してみたい。
- タンパク質結晶構造(
*.pdbフォーマット)から散乱曲線(*.datフォーマット)を計算しプロットする。 - 散乱曲線 \(I(q)\) から動径分布関数 \(P(r)\) 関数を計算し、出力ファイル(
*.outフォーマット)から \(P(r)\) 関数を抽出しプロットする。 - \(P(r)\) 関数からビーズモデルを計算する。シミュレーションデータ(
*.fitフォーマット)と元データを比較する。 - ビーズモデル(
*.pdb)と結晶構造(*.pdb)の比較
解析フローは 図 2.1 となる。
使用するデータ:
- タンパク質結晶構造
6lyz.pdb- タンパク質溶液散乱データ
lyzexp.dat[3]
2.4. 動径分布関数からビーズモデルを計算するプログラム SHAPES¶
小角散乱データからビーズモデルを計算するのは一般的に DAMMIN というプログラムが広く使用されている。これは \(I(q)\) に対してフィッテイングを行いビーズモデルを再構成計算する。本稿では、2019年に発表された SHAPES [4] による構造計算を行ってみよう。
SHAPES はJohn Badgerによって開発された \(P(r)\) 関数に対してフィッティングを行い、タンパク質分子構造を再構成するプログラムである。元のpythonコードは以下のサイトからフリーでダウンロードできる。
元々 SHAPES は単体でpythonコードを実行することを想定しているが、 jupyter-notebook 環境では使いにくいので変更を加えた。具体的には変数はセル上に入力して SHAPES をセル上から実行できるように SHAPES を本体部 shapes_main とモジュール部 shapes_module に分割した。
shapes_module は小角散乱を取り扱う上で便利なメソッドを含有している。 SHAPES 実行以外でも色々活用できる。その詳細を以下に示す。
| メソッド名 | 内容 |
|---|---|
ft_to_intensity |
動径分布関数 \(P(r)\) 関数から散乱強度 \(I(q)\) の計算 |
score_Ic |
入力散乱強度 \(I(q)\) と出力散乱強度 \(I_{calc}(q)\) のスケーリングと比較 |
write_all_data |
入力データと出力データを書き込む |
read_i |
GNOM 出力データから散乱強度データを読み取る |
read_pdb |
初期PDBファイルを読み取る |
pr_writer |
計算された \(P(r)\) データをファイルに書き込む |
pdb_writer |
ビーズの位置情報をPDBファイル形式で書き込む |
set_box |
概念的な格子上のローカルビーズ密度と点密度を評価する |
set_vol |
分子体積の設定 |
disallowed_beads |
許容体積内にないビーズを見つける |
calc_pr |
\(P(r)\) 関数の計算 |
pr_dif |
入力 \(P(r)\) とモデル \(P(r)\) のrms差のスコア |
pr_rfactor |
入力 \(P(r)\) とモデル \(P(r)\) の残差の統計 |
vdw_energy |
ビーズ間の相互作用エネルギーを計算する |
random_beads |
最大長 \(D_{max}\) の格子にビーズをランダムに配置する |
read_pr |
GNOM 出力ファイルから \(P(r)\) 関数を抽出する |
scale_pr |
入力 \(P(r)\) 関数と出力 \(P(r)\) をスケーリング |
get_dr |
2つの座標間の0以外の距離を返す |
center_beads |
半径内のビーズの中心を見つける |
get_total_energy |
総 vdw エネルギーの平均を取得 |
e_min |
エネルギーを最小化する |
make_symm |
対称性に関係するパラメータを設定する |
pr_shift_atom |
ビーズの位置を変更するための \(P(r)\) のシフトベクトルを設定する |
recenter_pdb |
元のビーズセットを原点に移動 |
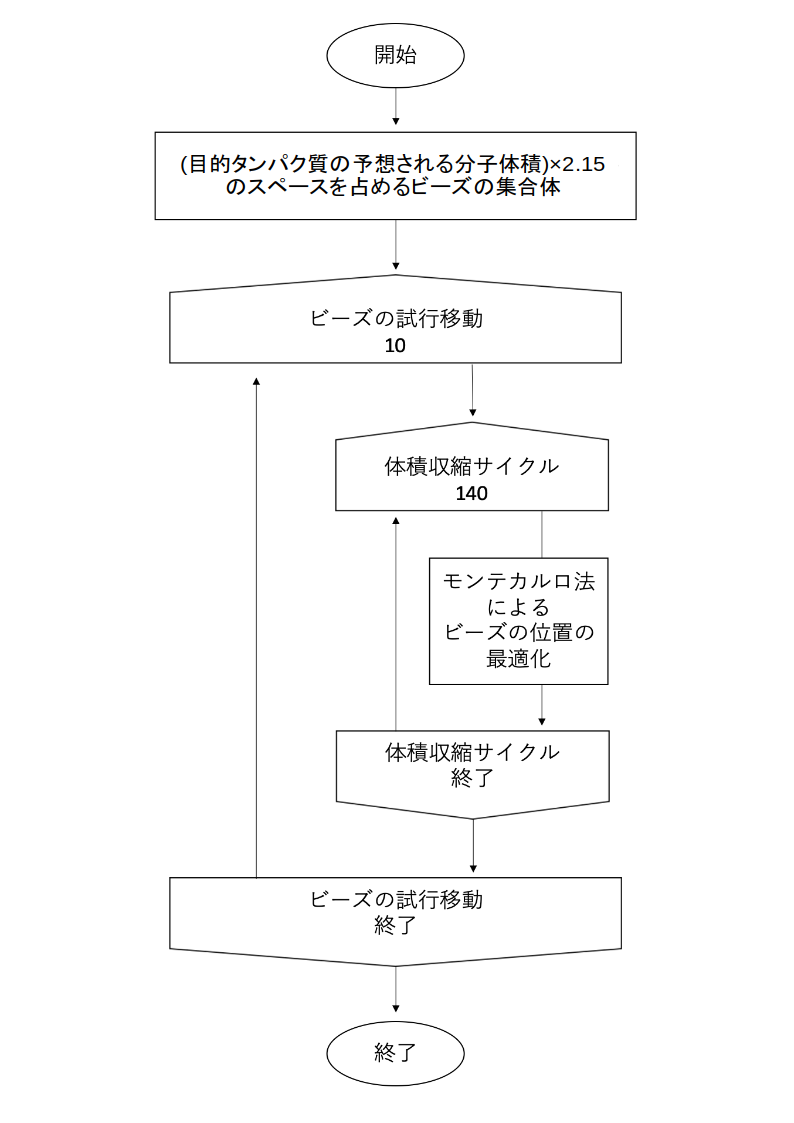
SHAPES のアルゴリズムは以下のようである。
このプログラムはビーズ間のポテンシャル関数として変形レナード・ジョーンズポテンシャル を用いて、ビーズの位置の最適化を試みる。
2.4.1. SHAPES の入力パラメータ¶
SHAPES で使用されるパラメータとその内容を以下に示す。
| パラメータ名 | 内容 | デフォルト |
|---|---|---|
nbeads_h |
構造内のアミノ酸の総数 | なし・入力必須 |
inFile_h |
ATSASパッケージの GNOM による出力としての \(P(r)\) ファイル | なし・入力必須 |
num_sols |
再構成の実行回数 | 4回 |
num_aa |
計算に使用されるビーズの数を変更するために使用するアミノ酸数のスケール | 1.0 |
num_symm |
タンパク質集合体の回転対称性 | 1 |
bias_z_h |
Z軸に沿ってビーズの初期構成を偏らせる | 0.0 |
inflate |
予想される部分比容に関連して、開始体積と最終体積を調整するためのスケール係数 | 1.0 |
pdbfile_in_h |
入力PDBファイルから読み取られたCα原子を使用して、再構成プロセスを開始する | none |
surface_scale |
再構成手順を安定させ、より連続した体積を持ち互いに類似した再構成をもたらす | 0.0 |
分子体積[ \(\mathrm{\mathring{A}^3}\) ]は入力されたアミノ酸数から推定される。アミノ酸あたり110Daを想定し、分子量と分子体積の間の変換係数として1.21を使用する。